Vektor dimensi dua adalah vektor yang mempunyai dua unsur yaitu unsur vertikal (sumbu Y) dan horizontal (sumbu X). Vektor pada bidang datar (dimensi dua) ditandai dengan sumbu X dan sumbu Y, yang saling berpotongan di titik pusat O (0, 0)

Daftar Isi

Vektor dimensi dua adalah vektor yang mempunyai dua unsur yaitu unsur vertikal (sumbu Y) dan horizontal (sumbu X). Vektor pada bidang datar (dimensi dua) ditandai dengan sumbu X dan sumbu Y, yang saling berpotongan di titik pusat O (0, 0). Secara analitis vektor dimensi dua dapat disajikan menurut unsur-unsurnya yaitu:

Dengan x adalah unsur mendatar. Apabila $x > 0$ (positif) maka x mempunyai arah ke kanan dan apabila $x < 0$ (negatif) x mempunyai arah ke kiri. Selanjutnya y adalah unsur vertikal. Apabila $y > 0$ (positif) maka arahnya ke atas dan jika $y < 0$ (negatif) arahnya ke bawah.

1. Komponen Vektor, Vektor Kolom, dan Vektor Baris

Perhatikan vektor pada gambar berikut 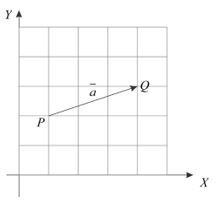Vektor Kolom Secara umum vektor $\vec{a}$ pada gambar diatas dapat ditulis secara kolom sebagai berikut $$\vec{PQ}=\vec{a}=\begin{pmatrix} 3 \\ 1 \end{pmatrix}$$ selain dengan vektor kolom, vektor $\vec{a}$ juga dapat ditulis dengan vektor baris seperti berikut $$\vec{PQ}=\vec{a}=\begin{pmatrix} 3, 1\end{pmatrix}$$

$\begin{pmatrix} 3 \\ 1 \end{pmatrix}$ disebut Vektor kolom dan $\begin{pmatrix} 3, 1\end{pmatrix}$ disebut vektor baris. 3 dan 1 merupakan komponen dari Vektor $\vec{a}$.

Vektor yang digambarkan pada bidang koordinat mempunyai komponen horisontal (gerakan ke kanan/kiri) dan komponen vertikal (gerakan ke atas/bawah). Oleh karena itu, vektor dapat disajikan secara kolom. 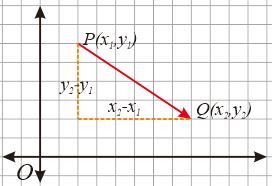Komponen Vektor $$\vec{PQ}=\begin{pmatrix} \text{Komponen horisontal} \\ \text{komponen vertikal}\end{pmatrix}$$

2. Vektor Posisi

Vektor Posisi adalah vektor yang berpangkal di pusat koordinat $O(0,0)$ dan berujung di suatu titik $(x,y)$. Perhatikan sebarang titik $A(x_1, y_1)$ dan titik $B(x_2, y_2)$ pada koordinat Cartesius berikut. 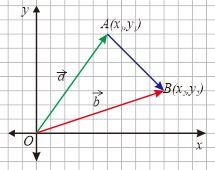Vektor Posisi Pada gambar di atas, vektor $\vec{a}$ mewakili ruas garis berarah dari titik pangkal $O(0, 0)$ ke titik $A(x_1, y_1)$ atau vektor $\vec{OA}$. Oleh karena itu, vektor $\vec{a}$ dapat dituliskan dalam bentuk vektor kolom
$\vec{OA}=\vec{a} = \begin{pmatrix} x_1 \\ y_1 \end{pmatrix}$
Adapun vektor $\vec{b}$ mewakili ruas garis berarah dari titik pangkal $O(0, 0)$ ke titik $B(x_2, y_2)$ atau vektor $\vec{OB}$. Vektor $\vec{b}$ dapat dituliskan sebagai
$\vec{OB}=\vec{b} = \begin{pmatrix} x_2 \\ y_2 \end{pmatrix}$

Sekarang perhatikan vektor $\vec{AB}$. Vektor $\vec{AB}$ kita dapatkan dengan cara menarik garis dari titik A ke titik B. Seperti yang sudah dipelajari sebelumnya, vektor $\vec{AB}$ dapat dinyatakan dalam bentuk penjumlahan vektor secara geometri yaitu $\vec{AB}=\vec{OB}-\vec{OA}$ sehingga $$\begin{align*} \vec{AB}&=\vec{OB}-\vec{OA} \\ &=\vec{b}-\vec{a}\\ &= \begin{pmatrix}x_2\\y_2\end{pmatrix}-\begin{pmatrix}x_1\\y_1\end{pmatrix}\\ \vec{AB} &=\begin{pmatrix}x_2-x_1\\y_2-y_1\end{pmatrix} \end{align*}$$

3. Modulus atau Besar Vektor

Modulus menyatakan panjang atau besar vektor. Karena panjang atau besar vektor selalu bernilai positif maka cara menulis modulus menggunakan tanda mutlak $\left( \lvert {} \rvert \right)$. 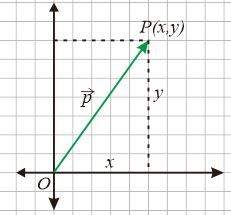Panjang Vektor Jika diketahui koordinat titik $P (x, y)$ maka panjang vektor posisi $\vec{OP}=\begin{pmatrix} x \\ y \end{pmatrix}$ dirumuskan dengan dalil pythagoras atau sebagai berikut $\lvert \vec{OP} \rvert=\sqrt{x^2+y^2}$.

Contoh 1
Diketahui Vektor $\vec{OQ}=\vec{q}=\begin{pmatrix}3 \\4 \end{pmatrix}$. Tentukan Panjang Vektor $\vec{q}$

Alternatif penyelesaian
$$\begin{align*} & \lvert \vec{q} \rvert=\sqrt{3^2+4^2}\\ & \lvert \vec{q} \rvert=\sqrt{25}\\& \lvert \vec{q} \rvert=5\end{align*}$$ Jadi, Panjang Vektor $\vec{q}$ adalah 5 satuan

4. Vektor satuan

Pada pembahasan sebelumnya, vektor satuan dari vektor $\vec{a}$ dirumuskan: $e_{\vec{a}}=\frac{\vec {a}}{\lvert \vec{a} \rvert}$ atau $\widehat{a}=\frac{\vec{a}}{\lvert \vec{a} \rvert}$

Dalam Vektor kolom, jika $\vec{a}=\begin{pmatrix} x \\ y \end{pmatrix},$ maka $\widehat{a}=\frac{1}{\sqrt{x^2+y^2}}.\begin{pmatrix} x \\ y \end{pmatrix}$

5. Sifat Operasi Vektor kolom

a. Penjumlahan Vektor

Secara analisis, Penjumlahan dua vektor dapat dikerjakan sebagai berikut
$$\vec{a}+\vec{b} = \begin{pmatrix} x_1 \\ y_1 \end{pmatrix}+\begin{pmatrix} x_2 \\ y_2 \end{pmatrix}=\begin{pmatrix} x_1+x_2 \\ y_1+y_2 \end{pmatrix}$$ Apabila kedua vektor diketahui mengapit sudut tertentu, maka dapat digunakan perhitungan dengan memakai rumus aturan cosinus seperti pada trigonometri. 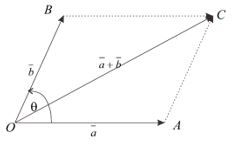Penjumlahan Vektor Apabila sudut antara $\vec{a}$ dan $\vec{b}$ adalah $\theta$, maka $$\begin{align*} {\lvert \vec{a}+\vec{b} \rvert}^2&=\lvert \vec{a} \rvert+\lvert \vec{b} \rvert+2\lvert \vec{a} \rvert\lvert \vec{b} \rvert \cos \theta \\ \lvert \vec{a}+\vec{b} \rvert&=\sqrt{\lvert \vec{a} \rvert+\lvert \vec{b} \rvert+2\lvert \vec{a} \rvert\lvert \vec{b} \rvert\cos \theta } \end{align*}$$

Jika vektor disajikan dalam bentuk komponen (dalam bidang kartesius) maka penjumlahan dapat dilakukan dengan menjumlahkan komponennya.

Misalnya:
$\vec{a} = \begin{pmatrix} x_A \\ y_A \end{pmatrix}$ dan $\vec{b}$ = $\begin{pmatrix} x_B \\ y_B \end{pmatrix}$ maka $\vec{a}+\vec{b} = \begin{pmatrix} x_A+x_B \\ y_A+y_B \end{pmatrix}$

Contoh 2
Diketahui vektor $\vec{a}=\begin{pmatrix} 2 \\ -3 \end{pmatrix}$ dan vektor $\vec{b}=\begin{pmatrix} -4 \\ 3 \end{pmatrix}$. Tentukan penjumlahan vektor dari $\vec{a}+\vec{b}$!
Alternatif Penyelesaian
$\vec{a}+\vec{b}$ = $\begin{pmatrix} 2+(-4) \\ -3+3 \end{pmatrix}=\begin{pmatrix} -2 \\ 0 \end{pmatrix}$

Contoh 3
Diketahui panjang vektor |$\vec{a}$| = 2 dan panjang vektor |$\vec{b}$| = 4, sudut antara vektor $\vec{a}$ dan $\vec{b}$ adalah $60^\circ$, maka :

$$\begin{align*}\lvert \vec{a}+\vec{b} \rvert&=\sqrt{\lvert \vec{a} \rvert+\lvert \vec{b} \rvert+2\lvert \vec{a} \rvert \lvert \vec{b} \rvert \cos \theta } \\ &= \sqrt{2^2+4^2+2.2.4.\cos 60^\circ} \\ &= \sqrt{4+16+16.\tfrac{1}2} \\ &= \sqrt{28}\\ &=2\sqrt{7} \end{align*}$$

b. Pengurangan Vektor

Secara analitis, jika diketahui Vektor $\vec{a}=\begin{pmatrix} a_1 \\ a_2 \end{pmatrix}$ dan $\vec{b}=\begin{pmatrix} b_1 \\ b_2 \end{pmatrix}$ maka pengurangan dua Vektor dapat dirumuskan $\vec{a}-\vec{b}=\begin{pmatrix} a_1-b_1 \\ a_2-b_2 \end{pmatrix}$ 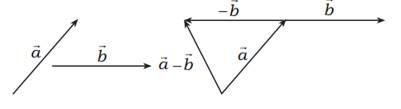Pengurangan Vektor Contoh 4 Diketahui vektor $\vec{p}=\begin{pmatrix} 6 \\ -3 \end{pmatrix}$ dan vektor $\vec{q}=\begin{pmatrix} -4 \\ 3 \end{pmatrix}$. Tentukan vektor dari $\vec{p}-\vec{q}$!
Alternatif Penyelesaian
$\vec{p}-\vec{q}$ = $\begin{pmatrix} 6-(-4) \\ -3-3 \end{pmatrix}=\begin{pmatrix} 10 \\ -6 \end{pmatrix}$

c. Perkalian Skalar dengan Vektor

Perkalian skalar dengan vektor akan menghasilkan vektor dengan arah yang sama. Vektor $\vec{v}$ sejajar dengan vektor $\vec{u}$, ditulis $\vec{v}//\vec{u}$ jika:

  • Jika $k > 0$, maka $\vec{v}$ searah $\vec{u}$
  • Jika $k < 0$, maka $\vec{v}$ berlawanan $\vec{u}$ Perkalian Vektor

Secara analitis, jika diketahui Vektor $\vec{a}=\begin{pmatrix} a_1 \\ a_2 \end{pmatrix}$maka $k.\vec{a}=\begin{pmatrix} k.a_1 \\ k.a_2 \end{pmatrix}$, dengan $k$ sebuah konstanta. Contoh 5
Diketahui $\vec{a} = \begin{pmatrix} -2 \\3 \\\end{pmatrix}$ dan $\vec{b} = \begin{pmatrix}4 \\-2 \\\end{pmatrix}$ tentukanlah $3\vec{b} – \frac{1}{2}\vec{a}$! Alternatif Penyelesaian
$$\begin{align*} 3\vec{b} – \frac{1}{2}\vec{a}&=3 \begin{pmatrix} -2 \\3 \\\end{pmatrix}-\frac{1}{2}\begin{pmatrix}4 \\-2 \\\end{pmatrix}\\ &= \begin{pmatrix} 3.(-2) \\3(3) \\\end{pmatrix}-\begin{pmatrix}\frac{1}{2}(4) \\\frac{1}{2}(-2) \\\end{pmatrix}\\&= \begin{pmatrix} -6 \\9 \\\end{pmatrix}-\begin{pmatrix}2 \\ -1 \\\end{pmatrix}\\&=\begin{pmatrix}-6-2 \\ 9-(-1) \\\end{pmatrix}\\&=\begin{pmatrix}-8 \\ 10 \\\end{pmatrix} \end{align*}$$ **Contoh 6**
Tentukan apakah titik-titik P(1, –2), Q(2, 1), dan R(4, 7) kolinear (segaris).
**Alternatif Penyelesaian:**
Titik P, Q dan R dikatakan kolinear (segaris) jika titik P, Q dan R terletak pada garis yang sama. Titik P, Q dan R akan terletak pada garis yang sama jika dan hanya jika vektor-vektor yang mewakili ruas garis berarah dari titik-titik P, Q dan R memiliki pangkal yang sama dan sejajar.
Vektor $\vec{PQ}$ dan $\vec{PR}$ memiliki titik pangkal yang sama.
Komponen vektor $\vec{PQ}=\vec{q}-\vec{p}=\begin{pmatrix}2 \\ 1 \end{pmatrix}-\begin{pmatrix}1 \\ -2 \end{pmatrix}=\begin{pmatrix}1 \\ 3 \end{pmatrix}$
Komponen vektor $\vec{PR}=\vec{r}-\vec{p}=\begin{pmatrix}4 \\ 7 \end{pmatrix}-\begin{pmatrix}1 \\ -2 \end{pmatrix}=\begin{pmatrix}3 \\ 9 \end{pmatrix}$

Dua vektor segaris jika ada bilangan $k$ yang memenuhi $\vec{PR}=k.\vec{PQ}$ dan kedua vektor berpangkal yang sama. $$\begin{align*} \vec{PR}&=\begin{pmatrix}3 \\ 9 \end{pmatrix}\\ &= 3\begin{pmatrix}1 \\ 3 \end{pmatrix}\\\vec{PR}&= 3\vec{PQ} \end{align*}$$ Karena $\vec{PR}=3\vec{PQ}$ berarti vektor $\vec{PQ}$ sejajar vektor $\vec{PR}$ dan sama-sama berpangkal di titik P. Jadi, dapat disimpulkan bahwa titik P, Q dan R merupakan titik-titik yang kolinear (segaris).

d. Kesamaan dua Vektor

Secara analitis, dua Vektor $\vec{a}=\begin{pmatrix} a_1 \\ a_2 \\ \end{pmatrix}$ dan $\vec{b}=\begin{pmatrix} b_1 \\ b_2 \\ \end{pmatrix}$ dikatakan sama jika dan hanya jika $a_1=b_1$ dan $a_2=b_2$

4. Basis Normal Standar

Definisi basis

Jika masing-masing vektor tersebut panjangnya 1 satuan dan saling tegak lurus , maka $\vec{v}_1,\vec{v}_2,\vec{v}_3,…,\vec{v}_n$ itu disebut basis normal standar dalam ruang $V$

Berdasarkan definisi tersebut maka kita dapat menyimpulkan bahwa vektor-vektor:

  1. $\widehat{i}=\begin{pmatrix} 1 \\0 \\\end{pmatrix}$ dan $\widehat{j}=\begin{pmatrix}0 \\1 \\\end{pmatrix}$ adalah basis normal standar dalam ruang vektor $R^2$ dengan $\widehat{i}$ dan $\widehat{j}$ masing-masing sejajar dengan sumbu X dan Y

  2. $\widehat{i}=\begin{pmatrix}1 \\0 \\0 \\\end{pmatrix},$ $\widehat{j}=\begin{pmatrix}0 \\1 \\0 \\\end{pmatrix}$ dan $\widehat{k}=\begin{pmatrix}0 \\0 \\1 \\\end{pmatrix}$adalah basis normal standar dalam ruang vektor $R^3$ dengan $\widehat{i}$, $\widehat{j}$ dan $\widehat{k}$ sejajar dengan sumbu X, Y, dan Z.

Dengan demikian, jika P sebuah titik (x,y) dan O(0,0), maka Vektor posisi $\vec{OP}$ dapat ditulis sebagai kombinasi dari dua Vektor basis $\vec{OP}=\vec{p}=\begin{pmatrix}x \\ y \\ \end{pmatrix}=x\begin{pmatrix} 1\\ 0\\ \end{pmatrix}+y\begin{pmatrix} 0\\ 1\\ \end{pmatrix}=x\widehat{i}+y\widehat{j}$

Contoh 7
Diketahui segitiga OAB dengan titik sudut: O(0, 0), A(3, 1) dan B(6, 5). $\vec{a}$ merupakan vektor posisi dari titik 𝐴 dan $\vec{b}$ vektor posisi dari titik 𝐵. Nyatakan vektor $\vec{a}$, $\vec{b}$ dan $\vec{AB}$ dalam bentuk vektor basis.
Alternatif penyelesaian:
$\vec{a}=x_1\widehat{i}+y_1\widehat{j}=3\widehat{i}+\widehat{j}$
$\vec{b}=x_1\widehat{i}+y_1\widehat{j}=6\widehat{i}+5\widehat{j}$
$\vec{AB}=\vec{b}-\vec{a}=(6\widehat{i}+5\widehat{j})-(3\widehat{i}+\widehat{j})=3\widehat{i}+4\widehat{j}$

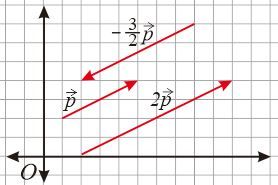
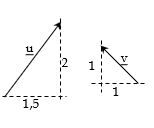
Latihan 3

  1. Perhatikan gambar vektor di samping :
    Gambarlah vektor Gambarlah vektor :
    1. $3.\vec{u}$
    2. $-2.\vec{v}$
    3. $\vec{u} + \vec{v}$
    4. $2.\vec{u} – \vec{v}$
  2. Jika diketahui $\vec{u} = \begin{pmatrix} 2 \\ 3 \end{pmatrix}$ dan $\vec{v} = \begin{pmatrix}-4 \\ 1 \end{pmatrix}$ tentukanlah :
    1. $\vec{u}$
    2. $-3.\vec{v}$
    3. $3.\vec{u} + 2.\vec{v}$
    4. $2.\vec{v} – \vec{u}$
  3. Diketahui vektor $\vec{a} = \begin{pmatrix}2 \\-1 \\\end{pmatrix}$ dan $\vec{b} = 2.\vec{a}$ , tentukanlah vektor $\vec{c} = \vec{a} + \vec{b}$
  4. Diketahui vektor $\vec{a} = \begin{pmatrix}-2 \\ 4 \\ \end{pmatrix}$, $\vec{b} = \begin{pmatrix} x \\ y \\ \end{pmatrix}$ dan c = $\begin{pmatrix}3 \\5 \\\end{pmatrix}$. Tentukan x dan y jika $\vec{c} = \vec{a} + \vec{b}$
  5. Jika vektor $\vec{m} = \begin{pmatrix}-8 \\4 \\\end{pmatrix}$ dan $\vec{n} = \begin{pmatrix}10 \\-6 \\\end{pmatrix}$ tentukanlah secara aljabar vektor dari :
    1. $\frac{1}{2} \vec{m} – \frac{1}{2} \vec{n}$
    2. $\frac{1}{4} \vec{m} + \frac{1}{2} \vec{n}$
  6. Diketahui $\vec{a} = \begin{pmatrix} -4 \\-2 \\\end{pmatrix}$ dan $\vec{b} = \begin{pmatrix}1 \\4 \\\end{pmatrix}$ tentukanlah $3\vec{b} – \frac{1}{2}\vec{a}$!
  7. Jika $\vec{a} = \begin{pmatrix}2 \\5 \\\end{pmatrix}$ dan $\vec{b} = \begin{pmatrix}3 \\-7 \\ \end{pmatrix}$ tentukanlah $2\vec{a} – \frac{1}{2}\vec{b}$!
  8. Jika $\vec{p} = \begin{pmatrix}5 \\-3 \\\end{pmatrix}$ dan $\vec{q} = \begin{pmatrix}4 \\-2 \\\end{pmatrix}$ tentukanlah $\frac{1}{2}\vec{b} – \frac{1}{2}\vec{q}$!
  9. Jika diketahui $\vec{p} = \begin{pmatrix}4 \\-6 \\\end{pmatrix}$ dan $\vec{q} = \begin{pmatrix}x \\y \\ \end{pmatrix}$ tentukanlah x dan y jika $\vec{p} + \vec{q} = \begin{pmatrix}-2 \\-3 \\ \end{pmatrix}$!
  10. Jika $\vec{a} = \begin{pmatrix}a_1 \\a_2 \\\end{pmatrix}$ dan $\vec{b} = \begin{pmatrix}-9 \\2 \\\end{pmatrix}$ tentukanlah $a_1$ dan $a_2$ jika $\vec{a} – \vec{b} = \begin{pmatrix}4 \\7 \\\end{pmatrix}$!