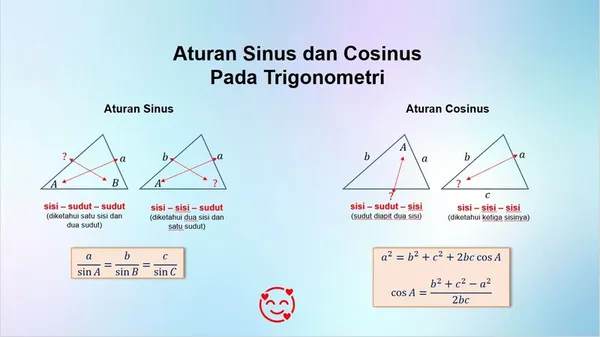
Aturan Sinus Dan Cosinus Trigonometri

Aturan Sinus berfungsi untuk menghubungkan sisi dan sudut segitiga. Aturan Cosinus adalah menghubungkan ketiga sisi ke satu sudut

Aturan Sinus adalah aturan penting yang berfungsi untuk menghubungkan sisi dan sudut segitiga. Sedangkan aturan Cosinus adalah menghubungkan ketiga sisi ke satu sudut. Aturan Sinus dapat digunakan dalam segitiga apapun dengan sisi dan sudut berlawanannya diketahui. Aturan Cosinus digunakan untuk menjelaskan hubungan antara nilai Cosinus dan kuadrat panjang sisi pada salah satu sudut segitiga.

Trigonometri tidak lepas dari segitiga, nah kali ini kita akan mempelajari aturan sinus dan aturan cosinus. Kita bisa mencari sudut dan sisi dari segitiga dengan menggunakan aturan ini. Seperti yang sudah dijelaskan diatas tadi. Agar lebih paham sebelumnya pelajari materi Perbandingan Trigonometri Pada Segitiga Siku-Siku↝ , Perbandingan Trigonometri Sudut Istimewa↝ , dan juga Nilai Perbandingan Trigonometri Di Berbagai Kuadran↝ .

1. Aturan Sinus

Penggunaan aturan sinus berlaku pada segitiga, termasuk segitiga siku-siku hingga segitiga sembarang. Perhatikan $\triangle ABC$ berikut. 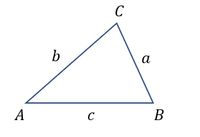Dari gambar di atas, berlaku aturan sinus yaitu : $$\begin{align*} \frac{a}{\sin \angle A} = \frac{b}{\sin \angle B} = \frac{c}{\sin \angle C} \end{align*}$$ atau $$\begin{align*} \frac{\sin \angle A }{a} = \frac{\sin \angle B}{b} = \frac{\sin \angle C}{c} \end{align*}$$

Pembuktian Rumus aturan sinus

Perhatikan gambar berikut.

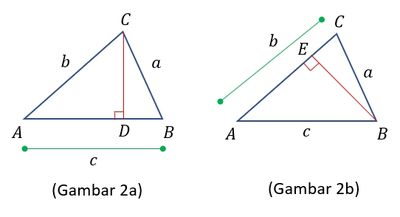
• Gambar (2a),

  • Dari $\triangle ADC$,
    $$\begin{align}\sin A = \frac{CD}{AC} \nonumber \\ \rightarrow CD = AC \sin A \nonumber \\ \rightarrow CD_1 = b \sin A \end{align}$$
  • Dari $\triangle BDC$,
    $$\begin{align}\sin B = \frac{CD}{BC} \nonumber \\ \rightarrow CD = BC \sin B \nonumber \\ \rightarrow CD_2 = a \sin B \end{align}$$
  • Dari persamaan (1) dan (2) atau panjang CD diperoleh,
    $$\begin{align}CD_1 = CD_2 \nonumber \\ \rightarrow b \sin A = a \sin B \nonumber \\ \rightarrow \frac{a}{\sin \angle A} = \frac{b}{\sin \angle B} \end{align}$$

• Dari gambar (2b),

  • Dari $\triangle AEB$, $$\begin{align} \sin A = \frac{EB}{AB} \nonumber \\ \rightarrow EB = AB \sin A \nonumber \\ \rightarrow EB_1 = c \sin A \end{align}$$
  • Dari $\triangle CEB$, $$\begin{align} \sin C = \frac{EB}{CB} \nonumber \\ \rightarrow EB = CB \sin C \nonumber \\ \rightarrow EB_2 = a \sin C \end{align}$$
  • Dari persamaan (4) dan (5) atau panjang EB diperoleh, $$\begin{align} EB_1 = EB_2 \nonumber \\ \rightarrow c \sin A = a \sin C \nonumber \\ \rightarrow \frac{a}{\sin \angle A} = \frac{c}{\sin \angle C} \end{align}$$

Dari pers(3) dan pers(6) diperoleh : $$\frac{a}{\sin \angle A} = \frac{b}{\sin \angle B} = \frac{c}{\sin \angle C}$$ Jadi, terbukti rumus aturan sinusnya.

Contoh Soal Aturan Sinus

1). Tentukan panjang AC pada segitiga berikut!

Alternatif Penyelesaian ✍️

Kita gunakan sudut A dan B untuk aturan sinusnya : $$\begin{align*} \frac{AC}{\sin B} &= \frac{BC}{\sin A} \\ \leftrightarrow \frac{AC}{\sin 60^\circ} &= \frac{12}{\sin 45^\circ} \\ \leftrightarrow \frac{AC}{\frac{1}{2}\sqrt{3}} &= \frac{12}{\frac{1}{2}\sqrt{2}} \\ \leftrightarrow \frac{AC}{\sqrt{3}} &= \frac{12}{\sqrt{2}} \\ \leftrightarrow AC &= \frac{12{\sqrt{3}}}{\sqrt{2}} \\ \leftrightarrow AC &= \frac{12{\sqrt{3}}}{\sqrt{2}}\cdot \frac{\sqrt{2}}{\sqrt{2}} \\ \leftrightarrow AC &= \frac{12{\sqrt{6}}}{2} \\ \leftrightarrow AC &= 6\sqrt{6} \end{align*}$$

Jadi, panjang $AC = 6 \sqrt{6}$ . 😄

2). Diberikan segitiga $KLM$ dengan panjang sisi $ML= 9$ cm dan $KL = 12$ cm. Sudut $M = 42^\circ$. Tentukan besar sudut K ! (gunakan bahwa $\sin 42^\circ = 0,669$ dan $\cos 42^\circ = 0.743$)

Alternatif Penyelesaian ✍️

Diketahui 2 sisi 1 sudut yang saling berhadapan maka gunakan aturan sinus $$\frac{KL}{\sin M}=\frac{ML}{\sin K}$$

$$\begin{align*}\frac{KL}{\sin M}=\frac{ML}{\sin K}\\ \leftrightarrow \frac{12}{\sin 42^\circ}=\frac{9}{\sin K}\\ \leftrightarrow \frac{12}{0,669}=\frac{9}{\sin K}\\ \leftrightarrow \sin K=\frac{9\times0,669}{12}\\ \leftrightarrow \sin K \approx 0.50175\\ \leftrightarrow \ K \approx \arcsin{0.50175}\\ \leftrightarrow \ K \approx 30,1^\circ \end{align*}$$

Jadi besar sudut K adalah $30,1^\circ$

2. Aturan Cosinus

Aturan kosinus adalah teorema yang digunakan untuk menentukan panjang sisi depan suatu sudut dengan menggunakan hubungan dua panjang sisi pengapit sudut tersebut dan nilai kosinusnya.

Perhatikan $\triangle ABC$ berikut. Dari gambar di atas, berlaku aturan sinus yaitu : $$\begin{align*} a^2=b^2+c^2-2bc\cos A \\ b^2=a^2+c^2-2ac\cos B \\ c^2=a^2+b^2-2ab\cos C \end{align*}$$ atau untuk menentukan sudut gunakan rumus $$\begin{align*} \cos A=\frac{b^2+c^2-a^2}{2bc}\\ \cos B=\frac{a^2+c^2-b^2}{2ac} \\ \cos C=\frac{a^2+b^2-c^2}{2ab} \end{align*}$$

Pembuktian Rumus aturan sinus

Perhatikan gambar berikut.

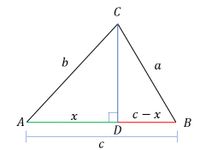
Perhatikan segitiga BCD dimana CD tegak lurus BD. Maka dengan menggunakan Teorema Phytagoras diperoleh bahwa: $$\begin{align*}CD^2=BC^2-BD^2 \\ \Rightarrow CD^2=a^2-(c-x)^2 \tag{1} \end{align*}$$

Perhatikan segitiga ACD dimana CD tegak lurus AD. Maka dengan menggunakan Teorema Phytagoras diperoleh bahwa: $$\begin{align*}CD^2=AC^2-BD^2 \\ \Rightarrow CD^2=b^2-x^2 \tag{2} \end{align*}$$

Ingatlah kembali bahwa: $$\begin{align*}\cos A=\frac{AD}{AC}\\ \Rightarrow \cos A=\frac{x}{b} \\ \Rightarrow b =x \cos A \tag{3} \end{align*}$$

Berdasarkan Pers. (1) dan (2) maka $$\begin{align*}CD^2&=CD^2 \\ \Rightarrow a^2-(c-x)^2&=b^2-x^2 \\ \Rightarrow a^2-(c^2-2cx+x^2)&=b^2-x^2 \\ \Rightarrow a^2-c^2+2cx-x^2&=b^2-x^2 \\ \Rightarrow a^2&=b^2+c^2-2cx \tag{4} \end{align*}$$

Substitusikan Pers. (3) ke Pers. (4) $$\begin{align*} a^2&=b^2+c^2-2cx \\ \Rightarrow a^2&=b^2+c^2-2cb \cos A \\ \Rightarrow a^2&=b^2+c^2-2bc \cos A \end{align*}$$

Dengan cara sama seperti di atas, dengan membuat garis tinggi dari masing-masing tiitk sudut yang lainnya yaitu AC dan BC maka akan diperoleh aturan cosinus untuk sisi-sisi yang lain sebagai berikut: $$b^2=a^2+c^2-2ac\cos B \\ c^2=a^2+b^2-2ab\cos C$$

Jadi, terbukti rumus aturan cosinusnya.

Contoh Soal Aturan Cosinus

1). Tentukan panjang AB pada segitiga berikut!

Alternatif Penyelesaian ✍️

Berdasarkan aturan cosinus : $$\begin{align*} AB^2&=AC^2+BC^2-2.AC.BC \cos C \\ AB^2&=10^2+6^2-(2)(10)(6) \cos 60\degree \\ AB^2&=100+36-120. \frac{1}{2} \\ AB^2&=100+36-60 \\ AB^2&=76 \\ AB&=\sqrt{76} \\ AB&=\sqrt{4}\times\sqrt{19} \\ AB&=2\sqrt{19}\end{align*}$$

Jadi, panjang $AB = 2 \sqrt{19}$ . 😄

2). Diketahui segitiga ABC dengan panjang $AB=12$ cm, $AC=8$ cm, dan besar sudut $A=30\degree$. Maka tentukan panjang sisi BC?

Alternatif Penyelesaian ✍️

Diketahui 1 sudut diapit 2 sisi maka gunakan aturan cosinus $$a^2=b^2+c^2-2bc\cos A$$

$$\begin{align*} BC^2&=AB^2+AC^2-2.AB.AC \cos A \\ BC^2&=12^2+8^2-(2)(12)(8) \cos 30\degree \\ BC^2&=144+64-192. \frac{1}{2}\sqrt{3} \\ BC^2&=208-96\sqrt{3} \\ BC&=\sqrt{208-96\sqrt{3}}\end{align*}$$

Jadi, panjang $BC = \sqrt{208-96\sqrt{3}}$ . 😄