Belajar Konsep Jarak Pada Dimensi Tiga mulai dari Jarak Dua Titik, Jarak Titik ke Garis, Jarak Titik ke Bidang, Rumus hingga Contohnya
Daftar Isi
Setelah mempelajari materi kedudukan titik, garis, dan bidang pada bangun ruang↝ , kita lanjutkan lagi materi berikutnya yang berkaitan dengan dimensi tiga yaitu materi Konsep Jarak Titik pada Dimensi Tiga atau Bangun Ruang. Menentukan atau penghitungan jarak pada dimensi tiga merupakan salah satu materi yang ada pada Matematika jenjang SMA.
Untuk memudahkan mempelajari materi Konsep Jarak pada Dimensi Tiga atau Bangun Ruang, hal mendasar yang harus kita kuasai terlebih dahulu adalah teorema phytagoras, aturan cosinus pada segitiga, Cara Proyeksi Titik, Garis, dan Bidang, dan tentunya konsep segitiga lainnya seperti luas segitiga, dan juga sudut-sudut segitiga. Tidak semudah teori ya untuk dimensi tiga ini, kita harus bisa membayangkan proyeksi-proyeksinya. Untuk berhasil kita harus coba …. dan coba lagi… Kita harus percaya pada apa yang kita kerjakan.
Pada artikel ini yang kita bahas hanya sebatas jarak titik ke titik, jarak titik ke garis, dan jarak titik ke bidang. Sebelum mempelajari lebih lanjut perhatikan ilustrasi berikut
Seseorang akan merancang instalasi listrik di suatu daerah. Bagaimana menentukan jarak antara dua bagian gedung yang satu dengan lainnya agar dapat ditentukan misalnya kebutuhan kabel untuk keperluan tertentu? Bagaimana menentukan jarak antara kabel jaringan arus kuat yang melintasi bangunan-bangunan agar medan listrik tidak mengganggu penghuninya maupun alat-alat elektronik di dalamnya? perlu dipahami pengertian dan cara menentukan jarak antara dua benda.
Definisi
1. Konsep Jarak Secara Umum dalam Dimensi Tiga
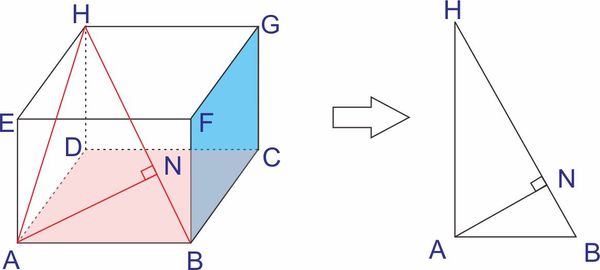
Misalkan diketahui balok ABCD.EFGH kita dapat menentukan jarak titik A ke garis BH dengan cara mmemroyeksikan titik A ke garis BH. Kita dapat menentukan jarak tersebut dengan membuat segitiga bantu ya..
2. Jarak Titik ke Titik pada Bangun Ruang atau Dimensi Tiga
Contoh Soal 1 Jarak Titik ke Titik pada Bangun Ruang atau Dimensi Tiga
Diketahui kubus ABCD.EFGH dengan panjang rusuk 8 cm. Hitunglah jarak antara titik-titik berikut.
- B ke F
- A ke D
- G ke H
- A ke C
- H ke B
- G ke titik tengah AB
Penyelesaian
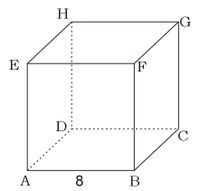
- Jarak titik B ke F diwakili oleh panjang ruas garis (rusuk) BF. Jadi, jarak titik B ke F adalah 8 cm.
- Jarak titik A ke D diwakili oleh panjang ruas garis (rusuk) AD. Jadi, jarak titik A ke D adalah 8 cm.
- Jarak titik G ke H diwakili oleh panjang ruas garis (rusuk) GH. Jadi, jarak titik G ke H adalah 8 cm.
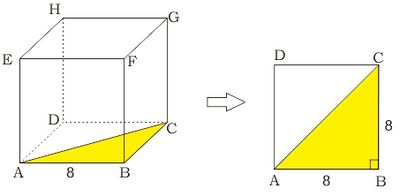
- Jarak titik A ke C diwakili oleh panjang ruas garis AC. Ruas garis AC merupakan diagonal bidang alas ABCD.
 Dari gambar di atas, kita perhatikan bahwa segitiga ABC adalah segitiga siku-siku di B. Berdasarkan Teorema Pythagoras diperoleh hubungan:
$$\begin{align*}\tag{teorema pythagoras}AC^2&=AB^2+BC^2\\ \tag{panjang AB=BC=8} &=8^2+8^2\\&=64+64\\&=64\times 2\\ AC&=\sqrt{64\times 2}=\sqrt{64}\times\sqrt{2}\\ AC &=8\sqrt{2} \end{align*}$$
Jadi, jarak titik A ke C adalah $8\sqrt{2}$ cm.
Dari gambar di atas, kita perhatikan bahwa segitiga ABC adalah segitiga siku-siku di B. Berdasarkan Teorema Pythagoras diperoleh hubungan:
$$\begin{align*}\tag{teorema pythagoras}AC^2&=AB^2+BC^2\\ \tag{panjang AB=BC=8} &=8^2+8^2\\&=64+64\\&=64\times 2\\ AC&=\sqrt{64\times 2}=\sqrt{64}\times\sqrt{2}\\ AC &=8\sqrt{2} \end{align*}$$
Jadi, jarak titik A ke C adalah $8\sqrt{2}$ cm. - Jarak titik B ke H diwakili oleh panjang ruas garis BH. Ruas garis BH merupakan diagonal ruang kubus ABCD.EFGH.
 Dari gambar, kita peroleh $\vartriangle BDH$ adalah segitiga siku-siku di D. BD merupakan diagonal bidang alas dengan panjang sama dengan AC sehingga $BD=AC=8\sqrt{2}$. Berdasarkan Teorema Pythagoras pada $\vartriangle BDH$ diperoleh hubungan:
$$\begin{align*}\tag{teorema pythagoras}BH^2&=BD^2+DH^2\\ &=(8\sqrt{2})^2+8^2\\&=128+64\\&=192=64\times 3\\ AC&=\sqrt{64\times 3}=\sqrt{64}\times\sqrt{3}\\ AC &=8\sqrt{3} \end{align*}$$
Jadi, jarak titik B ke H adalah $8\sqrt{3}$ cm.
Dari gambar, kita peroleh $\vartriangle BDH$ adalah segitiga siku-siku di D. BD merupakan diagonal bidang alas dengan panjang sama dengan AC sehingga $BD=AC=8\sqrt{2}$. Berdasarkan Teorema Pythagoras pada $\vartriangle BDH$ diperoleh hubungan:
$$\begin{align*}\tag{teorema pythagoras}BH^2&=BD^2+DH^2\\ &=(8\sqrt{2})^2+8^2\\&=128+64\\&=192=64\times 3\\ AC&=\sqrt{64\times 3}=\sqrt{64}\times\sqrt{3}\\ AC &=8\sqrt{3} \end{align*}$$
Jadi, jarak titik B ke H adalah $8\sqrt{3}$ cm. - Misal T adalah titik tengah AB maka jarak G ke titik tengah AB diwakili oleh panjang ruas garis TG
 Dari gambar, kita peroleh $\vartriangle TBG$ siku-siku di B. BG merupakan diagonal bidang dengan panjang sama dengan AC sehingga $BG=AC=8\sqrt{2}$. Berdasarkan Teorema Pythagoras pada $\vartriangle TBG$ diperoleh hubungan:
$$\begin{align*}\tag{teorema pythagoras}TG^2&=TB^2+BG^2\\ &=4^2+(8\sqrt{2})^2\\&=16+128\\&=144\\ AC&=\sqrt{144}\\ AC &=12 \end{align*}$$
Jadi, jarak titik G ke titik tengah AB adalah $12$ cm.
Dari gambar, kita peroleh $\vartriangle TBG$ siku-siku di B. BG merupakan diagonal bidang dengan panjang sama dengan AC sehingga $BG=AC=8\sqrt{2}$. Berdasarkan Teorema Pythagoras pada $\vartriangle TBG$ diperoleh hubungan:
$$\begin{align*}\tag{teorema pythagoras}TG^2&=TB^2+BG^2\\ &=4^2+(8\sqrt{2})^2\\&=16+128\\&=144\\ AC&=\sqrt{144}\\ AC &=12 \end{align*}$$
Jadi, jarak titik G ke titik tengah AB adalah $12$ cm.
Contoh Soal Sehari-hari, Jarak Titik ke Titik pada Bangun Ruang atau Dimensi Tiga
Pak Dimen mempunyai kamar tidur yang berukuran 3m × 3m × 4m. Tepat di tengah plafon kamar dipasang lampu. Jika saklar lampu diletakkan tepat di tengah salah satu dinding kamar, berapakah jarak dari lampu ke saklar?
Penyelesaian
Kita gambar dalam bentuk balok ABCD.EFGH
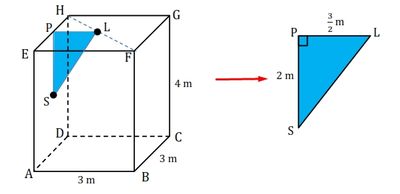 Misalkan lampu (L), saklar (S) berada di dinding ADHE, dan P adalah titik tengah EH. Jarak antara lampu dan saklar adalah LS.
Misalkan lampu (L), saklar (S) berada di dinding ADHE, dan P adalah titik tengah EH. Jarak antara lampu dan saklar adalah LS.
Perhatikan $\vartriangle LPS$ siku-siku di P. Dengan menggunakan teorema pythagoras kita peroleh $$\begin{align*}\tag{teorema pythagoras}LS^2&=PS^2+PL^2\\ &=2^2+\begin{pmatrix} \frac{3}{2} \end{pmatrix}^2\\&=4+\frac{9}{4}\\&=\frac{16}{4}+\frac{9}{4}=\frac{25}{4}\\ LS&=\sqrt{\frac{25}{4}}\\ LS &=\frac{5}{2}=2,5 \end{align*}$$ Jadi, jarak lampu ke saklar adalah $2,5$ cm.
3. Jarak Titik ke Garis pada Bangun Ruang atau Dimensi Tiga
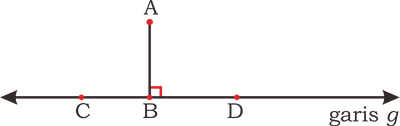
untuk menentukan jarak A ke garis g dapat dilakukan dengan cara
- Hubungkan titik A ke titik C dan ke titik D, sehingga terbentuk segitiga ACD
- Tetapkan jenis segitiga dengan melihat atau mencari panjang AC, AD dan CD.
- Hitung tinggi segitiga ACD, yaitu AB yang merupakan jarak titik A ke garis g
Ada 3 jenis segitiga ACD yang mungkin terbentuk. Berikut ini cara menghitung panjang ruas garis AB atau jarak titik A ke garis g.
- $\vartriangle$ ACD Sama Kaki
 $\vartriangle$ ACD sama kaki, sehingga
$\vartriangle$ ACD sama kaki, sehingga
$BC=BD=\frac{1}{2}CD$
Dengan Teorema Pythagoras diperoleh:
$AB^2=AD^2−(\frac{1}{2}CD)^2$
atau $AB^2=BD^2-BD^2$
atau $AB^2=CB^2-AC^2$ - $\vartriangle$ ACD Siku-siku di A
 Gunakan rumus Luas $\vartriangle$ ACD,
Gunakan rumus Luas $\vartriangle$ ACD,
$\text{Luas }\vartriangle ACD=\frac{1}{2}\times CD \times AB$ atau
$\text{Luas }\vartriangle ACD=\frac{1}{2}\times AC \times AD$
Sehingga diperoleh:
$A\frac{1}{2}\times CD \times AB=\frac{1}{2}\times AC \times AD$
$\Leftrightarrow CD \times AB=AC \times AD$
$\Leftrightarrow AB =\dfrac{AC \times AD}{CD}$ - $\vartriangle$ ACD Sembarang
 $x+y=AB \to y=AB-x$
$x+y=AB \to y=AB-x$
Rumus yang dipakai
$AB^2=AD^2-y^2$
atau
$AB^2=AC^2-x^2$
Contoh soal Jarak Titik ke Garis pada Bangun Ruang atau Dimensi Tiga
Diketahui kubus ABCD.EFGH dengan panjang rusuk 8 cm. Hitunglah jarak titik A ke garis HB.
Penyelesaian
Misalkan titik N merupakan proyeksi titik A terhadap garis HB sehingga ruas garis AN tegak lurus dengan HB maka jarak titik A ke HB merupakan ruas garis AN. Dengan menghubungkan titik A ke titik H dan titik A ke titik B diperoleh $\vartriangle ABH$ siku-siku di A dan AN garis tinggi.
Dengan menghubungkan titik A ke titik H dan titik A ke titik B diperoleh $\vartriangle ABH$ siku-siku di A dan AN garis tinggi.
Berdasarkan Teorema Pythagoras, AH merupakan diagonal bidang kubus berarti $AH=8\sqrt{2}$ cm dan HB merupakan diagonal ruang kubus, berarti $HB = 8\sqrt{3}$ cm.
Kita akan menghitung luas $\vartriangle ABH$ dalam dua sudut pandang, yaitu
$$\text{Luas }\vartriangle ABH=\frac{1}{2}\times AB \times AH $$ atau $$\text{Luas }\vartriangle ABH=\frac{1}{2}\times HB \times AN $$ sehingga diperoleh
$$ \cancel{\frac{1}{2}}\times AB \times AH = \cancel{\frac{1}{2}}\times HB \times AN\\ AB \times AH=HB \times AN \\ AN=\frac{AB \times AH}{HB}\\ \begin{align*}AN&=\frac{\cancel{8}\times 8\sqrt{2}}{\cancel{8}\sqrt{3}}\\ &=\frac{ 8\sqrt{2}}{\sqrt{3}}\times \frac{ \sqrt{3}}{\sqrt{3}}\\ AN &= \frac{8}{3}\sqrt{6} \end{align*}$$ Jadi, jarak titik A ke garis HB adalah $\dfrac{8}{3}\sqrt{6}$ cm.Diketahui limas segiempat beraturan T.ABCD dengan $AB = BC = 5\sqrt{2}$ cm dan TA = 13 cm. Hitung jarak titik A ke garis TC.
Alternatif Penyelesaian:
Misal P proyeksi titik A ke ruas garis TC.
Jarak titik A ke rusuk TC adalah AP. AC diagonal bidang alas, $AC=5\sqrt{2}.(\sqrt{2})=10$
AC diagonal bidang alas, $AC=5\sqrt{2}.(\sqrt{2})=10$
$$\begin{align*}OA&=OC=\frac{1}{2}AC=\frac12 .(10)=5\\ TO&=\sqrt{TC^2-OC^2}=\sqrt{13^2-5^2}\\&=\sqrt{169-25}=\sqrt{144}=12\end{align*}$$ untuk menentukan AP gunakan luas $\vartriangle TBC$ dari dua sudut pandang
$$\begin{align*}\cancel{\frac12} \times AC \times TO&=\cancel{\frac12} \times TC \times AP \\ AP&=\dfrac{AC\times TO}{TC}\\ AP&=\dfrac{10\times 12}{13}=\frac{120}{13} \end{align*}$$ Jadi, jarak titik A ke garis TC adalah $\frac{120}{13}$ cm.
4. Jarak Titik ke Bidang pada Bangun Ruang atau Dimensi Tiga
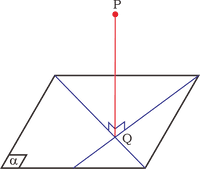
untuk menentukan jarak A ke bidang $\alpha$ dapat dilakukan dengan cara
- Dari titik P, tarik garis m yang tegak lurus terhadap bidang $\alpha$. Ingat garis m tegak lurus bidang $\alpha$ apabila garis m sedikitnya tegak lurus terhadap dua garis yang berpotongan pada bidang $\alpha$.
- Tentukan titik tembus garis m terhadap bidang $\alpha$ . Misalkan titik tembus ini adalah titik Q, jarak titik P ke bidang $\alpha$ adalah panjang ruas garis PQ.
Contoh soal Jarak Titik ke Bidang pada Bangun Ruang atau Dimensi Tiga
Diketahui kubus ABCD.EFGH dengan panjang rusuk 10 cm. Hitunglah jarak Titik A ke bidang BDE
Alternatif Penyelesaian:
Misal titik T adalah proyeksi titik A terhadap bidang BDE Perhatikan persegi panjang ACGE
Perhatikan persegi panjang ACGE
Garis AG berpotongan tegak lurus dengan Garis EO dititik T, sehingga jarak A ke Bidang BDE adalah AT. AC merupakan diagonal bidang alas maka $AC=10\sqrt2$.
$AO=OC=\frac12{AC}=5\sqrt2$
$$\begin{align*}EO^2&=AE^2+AO^2\\&=10^2+5\sqrt{2}^2\\&=100+50=150\\ EO&=\sqrt{150}\\ &= \sqrt{25\times 6}\\ EO&=5\sqrt6 \end{align*}$$ Perhatikan $\vartriangle AOE$ dari dua sudut, maka $$\begin{align*}\text{Luas }\vartriangle AOE =\cancel{\frac12}\times AO\times AE=\cancel{\frac12}\times EO\times AT\end{align*}\\ \Leftrightarrow AT=\frac{AO\times AE}{EO}\\\Leftrightarrow AT=\frac{5\sqrt2\times 10}{5\sqrt6}\\ AT=\frac{10}{\sqrt3}\\ AT=\frac{10}{3}\sqrt{3}$$ Jadi, jarak titik A ke bidang BDE adalah $\frac{10}{3}\sqrt{3}$ cm.Diketahui limas segiempat beraturan T.ABCD dengan $AB = BC = 5\sqrt{2}$ cm dan TA = 13 cm. Hitunglah
- jarak titik B ke bidang TAC.
- jarak titik T ke bidang ABCD.
Alternatif Penyelesaian:

- jarak titik B ke bidang TAC.
Misal O proyeksi titik T ke bidang ABCD. titik O merupakan pusat bidang ABCD. sehingga
Jarak titik B ke bidang TAC adalah BO.
$$\begin{align*}BO&=\frac12 BD\\ &=\frac12\sqrt{AB^2+AD^2} \\&=\frac12\sqrt{(5\sqrt{2})^2+(5\sqrt{2})^2}\\&=\frac12\sqrt{50+50}=\frac12\sqrt{100}\\ BO&=\frac12\times 10=5\end{align*}$$ Jadi, jarak titik A ke garis TC adalah $5$ cm. - jarak titik B ke bidang ABCD.
Jarak titik B ke bidang ABCD adalah tinggi limas T.ABCD yaitu TO.
$$\begin{align*}TO &=\sqrt{AT^2+AO^2} \\&=\sqrt{13^2-5^2}\\&=\sqrt{169-25}=\sqrt{144}\\ TO&=12\end{align*}$$ Jadi, jarak titik A ke garis TC adalah $12$ cm.
Demikian artikel mengenai konsep jarak titik pada bangun ruang. Silahkan dicoba untuk berlatih soal-soal yang lain yaa. Banyak sekali soal tentang konsep jarak ini. Tidak semudah teorinya. Ingat banyaklah berlatih biar lebih mahir.
 Dari gambar di atas, kita perhatikan bahwa segitiga ABC adalah segitiga siku-siku di B. Berdasarkan Teorema Pythagoras diperoleh hubungan:
$$\begin{align*}\tag{teorema pythagoras}AC^2&=AB^2+BC^2\\ \tag{panjang AB=BC=8} &=8^2+8^2\\&=64+64\\&=64\times 2\\ AC&=\sqrt{64\times 2}=\sqrt{64}\times\sqrt{2}\\ AC &=8\sqrt{2} \end{align*}$$
Jadi, jarak titik A ke C adalah $8\sqrt{2}$ cm.
Dari gambar di atas, kita perhatikan bahwa segitiga ABC adalah segitiga siku-siku di B. Berdasarkan Teorema Pythagoras diperoleh hubungan:
$$\begin{align*}\tag{teorema pythagoras}AC^2&=AB^2+BC^2\\ \tag{panjang AB=BC=8} &=8^2+8^2\\&=64+64\\&=64\times 2\\ AC&=\sqrt{64\times 2}=\sqrt{64}\times\sqrt{2}\\ AC &=8\sqrt{2} \end{align*}$$
Jadi, jarak titik A ke C adalah $8\sqrt{2}$ cm.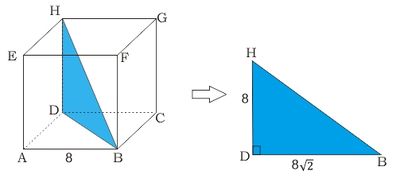 Dari gambar, kita peroleh $\vartriangle BDH$ adalah segitiga siku-siku di D. BD merupakan diagonal bidang alas dengan panjang sama dengan AC sehingga $BD=AC=8\sqrt{2}$. Berdasarkan Teorema Pythagoras pada $\vartriangle BDH$ diperoleh hubungan:
$$\begin{align*}\tag{teorema pythagoras}BH^2&=BD^2+DH^2\\ &=(8\sqrt{2})^2+8^2\\&=128+64\\&=192=64\times 3\\ AC&=\sqrt{64\times 3}=\sqrt{64}\times\sqrt{3}\\ AC &=8\sqrt{3} \end{align*}$$
Jadi, jarak titik B ke H adalah $8\sqrt{3}$ cm.
Dari gambar, kita peroleh $\vartriangle BDH$ adalah segitiga siku-siku di D. BD merupakan diagonal bidang alas dengan panjang sama dengan AC sehingga $BD=AC=8\sqrt{2}$. Berdasarkan Teorema Pythagoras pada $\vartriangle BDH$ diperoleh hubungan:
$$\begin{align*}\tag{teorema pythagoras}BH^2&=BD^2+DH^2\\ &=(8\sqrt{2})^2+8^2\\&=128+64\\&=192=64\times 3\\ AC&=\sqrt{64\times 3}=\sqrt{64}\times\sqrt{3}\\ AC &=8\sqrt{3} \end{align*}$$
Jadi, jarak titik B ke H adalah $8\sqrt{3}$ cm.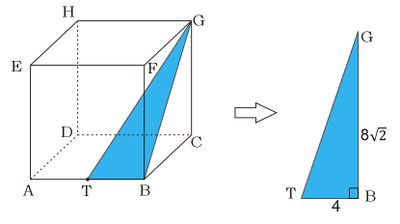 Dari gambar, kita peroleh $\vartriangle TBG$ siku-siku di B. BG merupakan diagonal bidang dengan panjang sama dengan AC sehingga $BG=AC=8\sqrt{2}$. Berdasarkan Teorema Pythagoras pada $\vartriangle TBG$ diperoleh hubungan:
$$\begin{align*}\tag{teorema pythagoras}TG^2&=TB^2+BG^2\\ &=4^2+(8\sqrt{2})^2\\&=16+128\\&=144\\ AC&=\sqrt{144}\\ AC &=12 \end{align*}$$
Jadi, jarak titik G ke titik tengah AB adalah $12$ cm.
Dari gambar, kita peroleh $\vartriangle TBG$ siku-siku di B. BG merupakan diagonal bidang dengan panjang sama dengan AC sehingga $BG=AC=8\sqrt{2}$. Berdasarkan Teorema Pythagoras pada $\vartriangle TBG$ diperoleh hubungan:
$$\begin{align*}\tag{teorema pythagoras}TG^2&=TB^2+BG^2\\ &=4^2+(8\sqrt{2})^2\\&=16+128\\&=144\\ AC&=\sqrt{144}\\ AC &=12 \end{align*}$$
Jadi, jarak titik G ke titik tengah AB adalah $12$ cm. $\vartriangle$ ACD sama kaki, sehingga
$\vartriangle$ ACD sama kaki, sehingga Gunakan rumus Luas $\vartriangle$ ACD,
Gunakan rumus Luas $\vartriangle$ ACD, $x+y=AB \to y=AB-x$
$x+y=AB \to y=AB-x$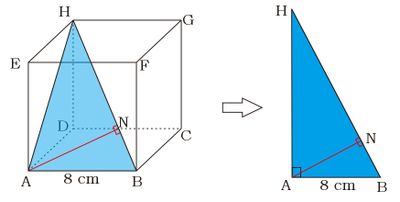 Dengan menghubungkan titik A ke titik H dan titik A ke titik B diperoleh $\vartriangle ABH$ siku-siku di A dan AN garis tinggi.
Dengan menghubungkan titik A ke titik H dan titik A ke titik B diperoleh $\vartriangle ABH$ siku-siku di A dan AN garis tinggi.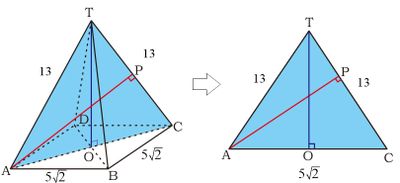 AC diagonal bidang alas, $AC=5\sqrt{2}.(\sqrt{2})=10$
AC diagonal bidang alas, $AC=5\sqrt{2}.(\sqrt{2})=10$ Perhatikan persegi panjang ACGE
Perhatikan persegi panjang ACGE