Pada artikel kali ini kita akan membahas beberapa penerapan vektor yaitu Resultan Vektor, Vektor Normal, Proyeksi Ortogonal Vektor, Jarak titik ke garis, dan Luas dan Volume.
Pada artikel kali ini kita akan membahas beberapa penerapan vektor yaitu Resultan Vektor, Vektor Normal, Proyeksi Ortogonal Vektor, Jarak titik ke garis, dan Luas dan Volume.
1. Resultan Dua Buah Vektor
Perhatikan gambar di samping berikut.
Diberikan dua buah vektor yaitu vektor $\vec{a}$ dan $\vec{b}$ serta sudut yang dibentuk oleh vektor $\vec{b}$ terhadap vektor $\vec{a}$ yaitu sebesar $\alpha $. Resultan dari vektor $\vec{a}$ dan $\vec{b}$ sama dengan mencari panjang OC.
Menggunakan aturan segitiga, panjang OC dapat kita cari dengan cara sebagai berikut. $$\left| \overrightarrow{OC} \right|^{2}={{\left| \overrightarrow{OA} \right|}^{2}}+{{\left| \overrightarrow{AC} \right|}^{2}}+2\left| \overrightarrow{OA} \right|\left| \overrightarrow{AC} \right|\cos \alpha $$ Dengan demikian resultan dua buah vektor $\vec{a}$ dan $\vec{b}$adalah: $$R=\sqrt{{{\left| \overrightarrow{a} \right|}^{2}}+{{\left| \overrightarrow{b} \right|}^{2}}+2\left| \overrightarrow{a} \right|\left| \overrightarrow{b} \right|\cos \alpha }$$ Selanjutnya, apabila resultan dari vektor $\vec{a}$ dan $\vec{b}$ yaitu vektor $\vec{r}$ membentuk sudut θ terhadap vektor $\vec{a}$ maka arah dari vektor resultan R dapat dicari dengan rumus sebagai berikut. $$\sin \theta =\frac{\left| \vec{b} \right|\sin \alpha }{R}$$
Contoh:
Sebuah kapal mengalami kemacetan di tengah laut. Untuk membawa kapal tersebut kembali ke pelabuhan dibutuhkan dua buah kapal penarik. Gaya yang dibutuhkan kedua kapal serta sudut yang dibentuk tampak pada gambar di samping. Tentukan besarnya resultan gaya yang dihasilkan kedua kapal!
Alternatif Penyelesaian:
Resultan gaya kedua kapal digambarkan pada diagram gaya di samping.
Resultan gaya kedua kapal diberikan sebagai berikut.
$$\begin{align*} & R=\sqrt{R_1^2+R_2^2+2R_1R_2\cos \alpha } \\ & R=\sqrt{{{80}^{2}}+{{105}^{2}}+2\cdot 80\cdot 105\cos 75{}^\circ } \\ & R\approx \sqrt{6.400+11.025+16.800\cdot 0,26} \\ & R\approx \sqrt{6.400+11.025+4.368} \\ & R\approx \sqrt{21.793} \\ & R\approx 147,62 \end{align*}$$
Jadi, resultan gaya kedua kapal adalah 147,62 N.
2. Vektor Normal Garis Lurus dalam R2 dan Normal Bidang dalam R3
Vektor normal dari suatu garis ialah vektor yang tegak lurus pada garis itu. Karena syaratnya asal tegak lurus, maka vektor normal itu dapat panjang, dapat pendek, asal bukan vektor nol. Biasanya vektor normal yang dipilih adalah vektor normal yang paling sederhana.
Dalil
$\vec{n}=\left( \begin{matrix} a \\ b \end{matrix} \right)\text{ tegak lurus garis }ax+by+c=0$ dalam ruang dimensi dua R2
$\vec{n}=\left( \begin{matrix} a \\ b \\ c \end{matrix} \right)\text{ tegak lurus garis }ax+by+cz+d=0$ dalam ruang dimensi tiga R3
3. Proyeksi Orthogonal suatu Vektor ke Vektor Lain
Proyeksi orthogonal suatu vektor ke vektor yang lain, hasilnya berupa vektor. Sedangkan panjang proyeksi vektor orthogonal suatu vektor pada vektor yang lain selalu bernilai bilangan/skalar real positif.
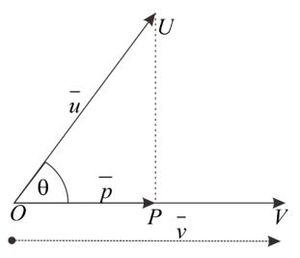Proyeksi orthogonal vektor $\vec{u}$ pada vektor $\vec{v}$ dapat dinotasikan oleh ${\vec{u}}_{\vec{v}}$ atau $\vec{p}$ dan ditentukan oleh dalil berikut.
Dalil :
- Proyeksi skalar orthogonal $\vec{u}$ pada $\vec{v}$ adalah $$\left| \left| \vec{p}\right| \right|=\frac{\vec{u}\cdot\vec{v}}{\left| \vec{v}\right|}$$
- Proyeksi vektor $\vec{u}$ ke vektor $\vec{v}$ adalah vektor $${\vec{u}}_{\vec{v}}=\left( \frac{\vec{u} \cdot \vec{v}}{\left| \vec{v} \right|^2} \right)\vec{v}\text{ atau } \vec{p}=\frac{\vec{u}}{\left| \vec{v} \right|} \left| \left| \vec{p} \right| \right|$$
- Panjang proyeksi vektor $\vec{u}$ ke vektor $\vec{v}$ adalah $$ \lvert \vec{u}_{\vec{v}}\rvert=\left| \vec{u}\cdot e_{\vec{v}} \right| $$ dengan $e_{\vec{v}}$ adalah vektor satuan ke arah $\vec{v}$ atau $\left| \vec{u}_{\vec{v}} \right|=\left| \frac{\vec{u}.\vec{v}}{\left| \vec{v} \right|} \right|$ .
Contoh 1:
Diketahui $\vec{a}=2\widehat{i}-6\widehat{j}-3\widehat{k}$ dan $\vec{b}=4\widehat{i}+2\widehat{j}-4\widehat{k}$. Tentukan:
- Panjang proyeksi vektor $\vec{a}$ pada $\vec{b}$
- Proyeksi orthogonal vektor $\vec{a}$ pada $\vec{b}$
- Proyeksi orthogonal vektor $\vec{b}$ pada $\vec{a}$
Alternatif Penyelesaan:
Panjang proyeksi vektor $\vec{a}$ pada $\vec{b}$ $$\begin{align*} \left| \vec{a}_{\vec{b}} \right|=\left| \frac{\vec{a}.\vec{b}}{\left| \vec{b} \right|} \right|&=\left| \frac{(2\widehat{i}-6\widehat{j}-3\widehat{k})\cdot (4\widehat{i}+2\widehat{j}-4\widehat{k})}{\sqrt{{{4}^{2}}+{{2}^{2}}+{{(-4)}^{2}}}} \right| \\ &=\left| \frac{(2)(4)+(-6)(2)+(-3)(-4)}{\sqrt{16+4+16}} \right| \\ &=\left| \frac{8-12+12}{\sqrt{36}} \right|=\left| \frac{8}{6} \right| \end{align*}$$ $ \therefore \left| \vec{a}_{\vec{b}} \right|=\frac{4}{3}$
Proyeksi orthogonal vektor $\vec{a}$ pada $\vec{b}$
$\vec{a}_{\vec{b}}=\left| \left| \vec{a}_{\vec{b}} \right| \right|\frac{\vec{b}}{\left| \vec{b} \right|}$, karena $\left| \vec{b} \right|=6$ dan $\left| \left| {{\vec{a}}_{\vec{b}}} \right| \right|=\frac{4}{3}$
$$\begin{align*} \vec{a}_{\vec{b}}&=\frac{4}{3}.\frac{4\widehat{i}+2\widehat{j}-4\widehat{k}}{6} \\ & =\frac{8}{9}\widehat{i}+\frac{4}{9}\widehat{j}-\frac{8}{9}\widehat{k} \end{align*}$$Proyeksi orthogonal vektor $\vec{b}$ pada $\vec{a}$
$$\begin{align*}\vec{b}_{\vec{a}}&=\left( \frac{\vec{b}\cdot \vec{a}}{{{\left| \vec{a} \right|}^{2}}} \right)\vec{a} \\ &=\frac{(4\widehat{i}+2\widehat{j}-4\widehat{k})\cdot (2\widehat{i}-6\widehat{j}-3\widehat{k})}{{{\left( \sqrt{{{2}^{2}}+{{(-6)}^{2}}+{{(-3)}^{2}}} \right)}^{2}}}(2\widehat{i}-6\widehat{j}-3\widehat{k}) \\ &=\frac{(4)(2)+(2)(-6)+(-4)(-3)}{{{2}^{2}}+{{(-6)}^{2}}+{{(-3)}^{2}}}(2\widehat{i}-6\widehat{j}-3\widehat{k}) \\ &=\frac{8}{49}(2\widehat{i}-6\widehat{j}-3\widehat{k}) \\ \vec{b}_{\vec{a}}&=\frac{16}{49}\widehat{i}-\frac{48}{49}\widehat{j}-\frac{24}{49}\widehat{k})\end{align*}$$
4. Jarak titik ke garis dalam R2 dan jarak titik ke bidang dalam R3
Dalil :
Pada ruang dimensi dua (R2) , jarak titik $P(x_1,y_1)$ ke garis $ax+by+c=0$ adalah $$d=\left| \frac{ax_1+by_1+c}{\sqrt{a^2+b^2}} \right|$$
Pada ruang dimensi tiga (R3) , jarak titik $P(x_1,y_1,z_1)$ ke garis $ax+by+cz+d=0$ adalah $$d=\left| \frac{ax_1+by_1+cz_1+d}{\sqrt{a^2+b^2+c^2}} \right|$$
Contoh
Tentukan jarak titik (7,1) ke garis 4x –3y +10 = 0!
Alternatif Penyelesaian
- Cara vektor
Normal garis g : 4x-3y+10 = 0 adalah $\vec{n}=\left( \begin{matrix}4\\-3 \end{matrix} \right)$
Pilih salah satu titik pada garis $4x-3y+10 = 0$ yang berkoordinat bulat, misal $(–1 ,2)$. $$\vec{u}=\left( \begin{matrix}7 \\ 1 \end{matrix} \right)-\left( \begin{matrix} -1 \\ 2\end{matrix} \right)=\left( \begin{matrix} 8 \\ -1 \end{matrix} \right)$$ Jarak titik ke garis yang dimaksud adalah: $$\begin{align*}& d=\left| \frac{\vec{u}.\vec{n}}{\left| \vec{n} \right|} \right| \\ & d=\left| \frac{\left( \begin{matrix} 8 \\ -1 \end{matrix} \right)\left( \begin{matrix} 4 \\ -3 \end{matrix} \right)}{\sqrt{4^2+(-3)^2}} \right|=\left| \frac{32+3}{5} \right|=7 \end{align*}$$ - Cara analitis
$$\begin{align*} & d=\left| \frac{ax_1+by_1+c}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \right|= \\ & d=\left| \frac{(4)(7)-3(1)+10}{\sqrt{4^2+3^2}} \right| \\ & d=\left| \frac{28-3+10}{\sqrt{25}} \right|=\frac{35}{5} \\ & d=7\end{align*}$$
5. Luas permukaan dan volume bangun ruang
Luas jajargenjang yang dibentuk oleh vektor $\vec{u}$ dan vektor $\vec{v}$ adalah $$\begin{align*} & L=\text{alas }\times \text{ tinggi} \\ & L=\left| \vec{u} \right|\left| \vec{v}\sin \theta \right| \\ & L=\left| \vec{u} \right|\left| \vec{v} \right|\sin \theta ,\text{ }0\le \theta \le 180 \end{align*}$$ Karena nilai $\sin \theta $ selalu positif maka $L=\left| \vec{u} \right|\left| \vec{v} \right|\sin \theta $ juga dapat ditulis $L=\left| \vec{u}\times \vec{v} \right|$.
Karena daerah segitiga tepat merupakan $\dfrac12$ dari daerah jajargenjang maka luas segitiga adalah: ${{L}_{\vartriangle }}=\frac{1}{2}\left| \vec{u}\times \vec{v} \right|$
Paralel Epipedum ialah benda ruang bersisi 6 yang sisi-sisi sejajarnya kongruen dan masing-masing sisinya berupa jajargenjang. Volum parallel epipedum yang dibentuk oleh 3 vektor $\vec{u},\text{ }\vec{v},$ dan $\vec{w}$ adalah: $$V=\left| \vec{u}\cdot (\vec{v}\times \vec{w}) \right|=\left| \vec{v}\cdot (\vec{u}\times \vec{w}) \right|=\left| \vec{w}\cdot (\vec{u}\times \vec{v}) \right|$$
Contoh:
Diketahui balok ABCD EFGH dengan AB = 6, BC = 5, dan CG = 4 terletak pada koordinat ruang R3 seperti yang ditunjukkan pada gambar. Tentukan luas bidang ACH!
Alternatif Penyelesaian
Dari gambar yang tersedia kita dapat menyatakan bahwa koordinat titik A(5, 0, 0) ; B(5, 6, 0) ; C(0, 6, 0) ; H(0, 0, 4) ; F(5, 6, 4) ; dan G(0, 6, 4). Dari data tersebut maka Luas bidang ACH
$$\begin{align*} & L=\frac{1}{2}\left| \overrightarrow{AC}\times \overrightarrow{AH} \right| \\ & L=\frac{1}{2}\left| (\vec{c}-\vec{a})\times (\vec{h}-\vec{a}) \right| \\ & L=\frac{1}{2}\left| \left( \begin{matrix} -5 \\ 6 \\0 \end{matrix} \right)\times \left( \begin{matrix} -5 \\ 0 \\ 4 \end{matrix} \right) \right|=\frac{1}{2}\left| \left( \begin{matrix} \left| \begin{matrix} 6 & 0 \\ 0 & 4 \end{matrix} \right| \\ \left| \begin{matrix}0 & 4 \\ -5 & -5 \end{matrix} \right| \\ \left| \begin{matrix}-5 & -5 \\ 6 & 0 \end{matrix} \right| \end{matrix} \right) \right|=\frac{1}{2}\left| \begin{matrix} 24 \\ 20 \\ 30 \end{matrix} \right| \\ & L=\left| \begin{matrix} 12 \\ 10 \\ 15 \end{matrix} \right|=\sqrt{{{12}^{2}}+{{10}^{2}}+{{15}^{2}}}=\sqrt{469}\approx 21,66 \end{align*}$$