Perbandingan Vektor Pada Ruas Garis

Perbandingan vektor ini sebenarnya sama dengan perkalian skalar dengan vektor yang sudah kita pelajari pada artikel Tafsiran Geometri Dari Kedudukan Dua Vektor Atau Lebih. Kali ini kita akan belajar lebih mendalam terkait dengan koordinat titik pembaginya.

Pada artikel ini kita akan belajar tentang Perbandingan Vektor pada Ruas Garis. Perbandingan vektor ini sebenarnya sama dengan perkalian skalar dengan vektor yang sudah kita pelajari pada artikel Tafsiran Geometri Dari Kedudukan Dua Vektor Atau Lebih↝ . Kali ini kita akan belajar lebih mendalam terkait dengan koordinat titik pembaginya.

Ada tiga hal yang akan kita pelajari pada materi Perbandingan Vektor yaitu bisa menentukan pembagian ruas garis dengan perbandingan m:n, menentukan rumus pembagian dalam bentuk vektor dan menentukan koordinat titik pembagi pada ruas garis dan vektor. Sebelum mempelajari materi ini teman-teman harus menguasai dulu materi vektor sebelumnya seperti konsep Vektor↝ , operasi vektor↝ , tafsiran geometri vektor↝ .

1. Pembagian ruas garis dengan perbandingan m:n

Suatu titik R membagi ruas garis $AB$ dengan perbandingan $m:n$ jika $AR:RB=m:n$. Dalam perbandingan $AR:RB=m:n$ terdapat dua kemungkinan letak titik R pada ruas garis AB, yaitu:

1. Titik R terletak diantara titik A dan B (membagi AB di dalam), $$\begin{align*} & AR:RB=m:n \\&AR:AB=m:(m+n) \end{align*}$$

2. Titik R terletak sebelum atau setelah titik A dan B (membagi AB di luar). $$\begin{align*} & AR:RB=m:-n \\&AR:AB=m:(m-n) \end{align*}$$

2. Rumus pembagian dalam bentuk Vektor

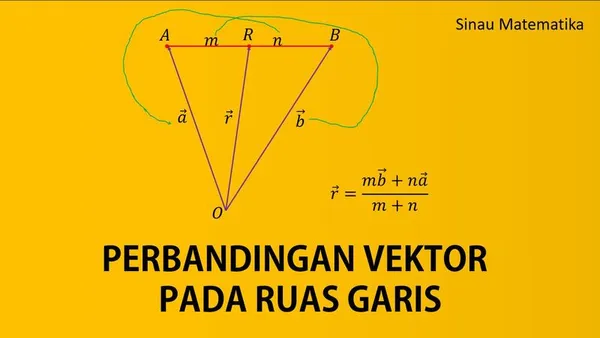
Pada gambar disamping, ARB adalah segaris (kolinear). $$\begin{align*} & AR:RB=m:n \\ &\Leftrightarrow \frac{AR}{RB}=\frac{m}{n}\\ &\Leftrightarrow nAR=mRB \end{align*}$$ Maka $$\begin{align*} & \text{}nAR=mRB \\ &\Leftrightarrow n(\vec{r}-\vec{a})=m(\vec{b}-\vec{r}) \\ &\Leftrightarrow \text{ }n\vec{r}-n\vec{a}=m\vec{b}-m\vec{r} \\ &\Leftrightarrow (m+n)\vec{r}=m\vec{b}+n\vec{a} \\ &\Leftrightarrow \text{ }\vec{r}=\frac{m\vec{b}+n\vec{a}}{m+n} \end{align*}$$

3. Rumus perbandingan dalam bentuk koordinat

Sebelumnya telah dirumuskan pembagian ruas garis dalam bentuk vektor, yaitu: $$\vec{r}=\frac{m\vec{b}+n\vec{a}}{m+n}$$ Maka

1. Jika $A(x_1,y_1)$ dan $B(x_2,y_2)$ di ${{R}^{2}}$, maka $$\vec{r}=\frac{m\left( \begin{matrix}x_2\\y_2\\\end{matrix} \right)+n\left( \begin{matrix}x_1\\y_1\\\end{matrix} \right)}{m+n}$$ Koordinat titik R adalah $R\left( \frac{mx_2+nx_1}{m+n},\text{ }\frac{my_2+ny_1}{m+n} \right)$
2. Jika $A(x_1,y_1,{z_1})$ dan $B(x_2,y_2,{z_2})$ di ${{R}^{2}}$, maka $$\vec{r}=\frac{m\left( \begin{matrix}x_2\\y_2\\z_2\\\end{matrix} \right)+n\left( \begin{matrix}x_1\\y_1\\z_1\end{matrix} \right)}{m+n}$$ Koordinat titik R adalah $R\left( \frac{mx_2+nx_1}{m+n},\text{ }\frac{my_2+ny_1}{m+n},\text{ }\frac{mz_2+nz_1}{m+n} \right)$

Contoh soal Perbandingan Vektor pada Ruas Garis

Contoh 1

Tentukan koordinat titik P yang membagi garis hubung $A(2,3,-1) $ dan $ B(-3,3, 4) $ dengan perbandingan $ 2 : 3 $ berdasarkan ketentukan :

1. Titik P membagi AB di dalam,
2. Titik P membagi AB di luar dan tentukan posisi letak titik P.

Penyelesaian :

1. Titik P membagi AB di dalam,
   • Bentuk perbandingannya adalah $\vec{AP} : \vec{PB} = 2 : 3 $
   • Menentukan vektor posisi titik P : $$\begin{align*} \vec{p} &= \frac{2\vec{b} + 3\vec{a}}{2+3} \\ &= \frac{1}{5} (2\vec{b} + 3\vec{a}) \\ &= \frac{1}{5} (2(-3,3, 4) + 3(2,3,-1)) \\ &= \frac{1}{5} ((-6,6, 8) + (6,9,-3)) \\ &= \frac{1}{5}(0,15, 5)\\ &=(0,3, 1) \end{align*}$$ Kita peroleh vektor posisi titik P yaitu $ \vec{p} =(0,3, 1)$ sehingga koordinat titik P adalah(0,3, 1).
2. Titik P membagi AB di luar dan tentukan posisi letak titik P.
   • Perbandingan vektornya $ m : n =2 : 3 $ artinya $ m < n $ sehingga titik P terletak sebelum garis AB.
   • Bentuk perbandingannya adalah $\vec{PA} : \vec{PB} = 2 : 3 $ atau $\vec{AP} : \vec{PB} = -2 : 3 $
   • Menentukan vektor posisi titik P : $$\begin{align*} \vec{p} &= \frac{-2\vec{b} + 3\vec{a}}{-2+3} \\&= \frac{-2\vec{b} + 3\vec{a}}{1} \\&= -2\vec{b} + 3\vec{a} \\&=-2(-3,3, 4) + 3(2,3,-1)\\&=(6,-6, -8) + (6,9,-3) \\&=(12,3, -11) \end{align*}$$ Kita peroleh vektor posisi titik P yaitu $ \vec{p} =(12,3, -11)$ sehingga koordinat titik P adalah $ (12,3, -11) $yang terletak sebelum titik A dan B.

Contoh 2

Tentukan koordinat titik C yang membagi garis hubung $P(2,-3,3) $ dan $ Q(2,4, 3) $ dengan perbandingan $ 5 : 2 $ berdasarkan ketentukan :

1. Titik C membagi PQ di dalam,
2. Titik C membagi PQ di luar dan tentukan posisi letak titik C.

Penyelesaian :

1. Titik C membagi PQ di dalam,
   • Bentuk perbandingannya adalah $\vec{PC} : \vec{CQ} = 5 : 2 $
   • Menentukan vektor posisi titik C : $$\begin{align*} \vec{c} &= \frac{5\vec{q} + 2\vec{p}}{5 + 2} \\ &= \frac{1}{7} (5\vec{q} + 2\vec{p}) \\&= \frac{1}{7} (5(2,4, 3) + 2(2,-3,3)) \\ &= \frac{1}{7} ((10,20, 15) + (4,-6,6)) \\ &= \frac{1}{7}(14,14, 21)\\&=(2 , 2, 3) \end{align*}$$ Kita peroleh vektor posisi titik C yaitu $ \vec{c} =(2 , 2, 3)$ sehingga koordinat titik C adalah(2 , 2, 3).
2. Titik C membagi PQ di luar dan tentukan posisi letak titik C.
   • Perbandingan vektornya $ m : n =5 : 2 $ artinya $ m > n $ sehingga titik C terletak setelah garis PQ.
   • Bentuk perbandingannya adalah $\vec{PC} : \vec{QC} = 5 : 2 $ atau $\vec{PC} : \vec{CQ} = 5 : -2 $
   • Menentukan vektor posisi titik C : $$\begin{align*} \vec{c} &= \frac{5\vec{q} - 2\vec{p}}{5 - 2} \\ &= \frac{1}{3} (5\vec{q} - 2\vec{p}) \\ &= \frac{1}{3} (5(2,4, 3) - 2(2,-3,3)) \\ &= \frac{1}{3} ((10,20, 15) - (4,-6,6)) \\ &= \frac{1}{3}(6,26,9)\\ &=\left(2,\frac{26}{3}, 3 \right) \end{align*}$$ Kita peroleh vektor posisi titik C yaitu $ \vec{c} =\left(2,\frac{26}{3}, 3 \right)$ sehingga koordinat titik C adalah $ \left(2,\frac{26}{3}, 3 \right)$yang terletak setelah titik P dan Q.

Contoh 3

Tentukan Koordinat titik P yang terletak di luar AB dengan $ A(-3, 2 , 1 ) $ , $ B( 1, -2, 4) $ $ \vec{AP} : \vec{PB} = 3 : (-2) $ dan tentukan letak titik P!

Penyelesaian :

• Pada perbandingan$ \vec{AP} : \vec{PB} = 3 : (-2) $, titik yang kembar (titik P) sudah ada ditengah sehingga tidak perlu kita balik arah vektornya. Untuk mengerjakannya langsung kita gunakan “dekat-dekat jauh-jauh”.
• Menentukan vektor posisi titik P : $$\begin{align*} \vec{p} &= \frac{3\vec{b} - 2\vec{a}}{3 - 2} \\ &= \frac{3\vec{b} - 2\vec{a}}{1} \\ &=3\vec{b} - 2\vec{a} \\ &=3( 1, -2, 4) - 2(-3, 2 , 1 ) \\ &=( 3, -6, 12) - (-6, 4 , 2 ) \\ &=( 9, -10, 10) \end{align*}$$ Kita peroleh vektor posisi titik P yaitu $ \vec{p} =( 9, -10, 10)$
  sehingga koordinat titik P adalah$ ( 9, -10, 10) $.
• Menentukan letak titik P apakah sebelum atau sesudah AB : Perhatikan perbandingan vektornya yaitu $ 3 : -2 $, jika kita mutlakkan maka kita peroleh perbandingannya menjadi $ 3 : 2 $, artinya $ m : n = 3 : 2 $ dimana memenuhi $ m > n $ sehingga titik P terletak setalah ruas garis AB.

Contoh 4

Bila $ \vec{a} $ , $ \vec{b} $ dan $ \vec{c} $ adalah vektor-vektor posisi dari titik A, B, dan C dari $ \Delta ABC $. Titik D pada $ \vec{AC} $ sehingga $ AD : DC = 1 : 3 $ . Titik E pada $ \vec{BC} $ sehingga $ BE : EC = 5 : 2 $. Nyatakan $ \vec{DE} $ dalam $ \vec{a} $ , $ \vec{b} $, dan $ \vec{c} $ !

Penyelesaian :

• Perhatikan ilustrasi gambar berikut :
  
• Menentukan vektor posisi D dengan perbandingan vektor $ AD : DC = 1 : 3 $ $$\begin{align*} \vec{d} &= \frac{1.\vec{c} + 3\vec{a} }{1 + 3}\\ &= \frac{\vec{c} + 3\vec{a} }{4} \end{align*}$$
• Menentukan vektor posisi E dengan perbandingan vektor $ BE : EC = 5 : 2$ $$\begin{align*} \vec{e} &= \frac{5\vec{c} + 2\vec{b} }{5 + 2}\\ &= \frac{5\vec{c} + 2\vec{b} }{7} \end{align*}$$
• Menentukan vektor $ \vec{DE} $ : $$\begin{align*} \vec{DE} &= \vec{e} - \vec{d}\\&= \frac{5\vec{c} + 2\vec{b} }{7} - \frac{\vec{c} + 3\vec{a} }{4} \\&= \frac{4(5\vec{c} + 2\vec{b}) }{28} - \frac{7(\vec{c} + 3\vec{a} )}{28} \\&= \frac{20\vec{c} + 8\vec{b} }{28} - \frac{7\vec{c} + 21\vec{a}}{28} \\&= \frac{20\vec{c} + 8\vec{b} - 7\vec{c} - 21\vec{a} }{28}\\&= \frac{- 21\vec{a} + 28\vec{b} - 7\vec{c} }{28}\\&= \frac{1}{28} ( - 21\vec{a} + 28\vec{b} - 7\vec{c}) \end{align*}$$ Jadi, hasilnya $ \vec{DE} = \frac{1}{28} ( - 21\vec{a} + 28\vec{b} - 7\vec{c})$.

Contoh 5

Dari segitiga ABC diketahui titik D pada AC dan E pada AB. Titik G pada perpotongan DB dan EC. Jika diketahui perbandingan $ AD : DC = 3 : 1 $ dan $ AE : EB = 1 : 2 $, maka tentukan perbandingan $ EG : GC $ dan $ DG : GB $ !

Penyelesaian :

• Perhatikan ilustrasi gambar berikut Pada gambar kita taris ruas garis AG . Untuk menentukan perbandingan garis yang diminta, kita akan kerjakan dengan menggunakan konsep perbandingan vektor.
• Dengan konsep titik-titik segaris (kolinear) , kita peroleh :
  Misalkan $ \vec{AB} = \vec{q} $ dan $ \vec{AC} = \vec{p} $.
  $ \vec{AE} = \frac{1}{3}\vec{AB} = \frac{1}{3}\vec{q} $ dan $ \vec{AD} = \frac{3}{4}\vec{AC} = \frac{3}{4}\vec{p} $.
  • Vektor $\vec{EG} $ segaris dengan $ \vec{EC} $ sehingga berlaku kelipatan :
    $ \vec{EG} = n\vec{EC} \rightarrow \frac{\vec{EG}}{\vec{EC}} = \frac{n}{1} $sehingga $ \frac{\vec{EG}}{\vec{GC}} = \frac{n}{1-n} $
  • Vektor $\vec{DG} $ segaris dengan $ \vec{DB} $ sehingga berlaku kelipatan :
    $ \vec{DG} = m\vec{DB} \rightarrow \frac{\vec{DG}}{\vec{DB}} = \frac{m}{1} $sehingga $ \frac{\vec{GG}}{\vec{GB}} = \frac{m}{1-m} $
• Menentukan vektor $ \vec{AG} $ dari $ \vec{EG}:\vec{GC} = n : 1-n $ $ \vec{AG} = \frac{n\vec{AC} + (1-n)\vec{AE}}{n + (1-n)} = \frac{n\vec{p} + (1-n).\frac{1}{3}\vec{q}}{1} = n\vec{p} + \frac{1-n}{3}\vec{q} $.
• Menentukan vektor $ \vec{AG} $ dari $ \vec{DG}:\vec{GB} = m : 1-m $ $ \vec{AG} = \frac{m\vec{AB} + (1-m)\vec{AD}}{m + (1-m)} = \frac{m\vec{q} + (1-m).\frac{3}{4}\vec{p}}{1} = m\vec{q} + \frac{3(1-m)}{4}\vec{p} $.
• Vektor $ \vec{AG} $ dari kedua bentuk di atas sama sehingga dengan menyamakan koefisien vektor sejenis, kita peroleh persamaan :
  • Koefisien vektor $ \vec{p} $ : $$ n = \frac{3(1-m)}{4} \rightarrow 4n = 3 - 3m \rightarrow 4n + 3m = 3 ….(1)$$
  • Koefisien vektor $ \vec{q} $ : $$ \frac{1-n}{3} = m \rightarrow 1 - n = 3m \rightarrow n + 3m = 1 ….(2)$$
  • Eliminasi pers(1) dan pers(2) : $$ \begin{array}{cc}4n + 3m = 3 &\\ n + 3m = 1 & -\\\hline 3n = 2 &\\ n = \frac{2}{3} \end{array} $$ Pers(2): $ n + 3m = 1 \rightarrow \frac{2}{3} + 3m = 1 \rightarrow m = \frac{1}{9} $.
• Menentukan perbandingan yang diminta :
  • Perbandingan $\vec{EG}:\vec{GC} $ $$\vec{EG}:\vec{GC} = n : 1-n = \frac{2}{3} : 1 - \frac{2}{3} = \frac{2}{3} : \frac{1}{3} = 2 : 1 $$
  • Perbandingan $ \vec{DG}:\vec{GB}$ : $$ \vec{DG}:\vec{GB} = m : 1-m= \frac{1}{9} : 1 - \frac{1}{9} = \frac{1}{9} : \frac{8}{9} = 1 : 8 $$

Jadi, kita peroleh perbandingan $ EG : GC = 2 : 1 $ dan $ DG : GB = 1 : 8 $.

Catatan : Untuk cara yang lebih efektif dalam mengerjakan contoh soal nomor 5 ini, kita bisa menggunakan dalil menelaus. Caranya yaitu :

• Menentukan perbandingan $ EG : GC $ : $$\begin{align*} \frac{EG}{GC}.\frac{CD}{DA}.\frac{AB}{EB} &= 1\\\frac{EG}{GC}.\frac{1}{3}.\frac{3}{2} &= 1\\\frac{EG}{GC}.\frac{1}{2} &= 1\\\frac{EG}{GC}&= 1 : \frac{1}{2} \\\frac{EG}{GC}&= \frac{2}{1} \end{align*}$$
• Menentukan perbandingan $ DG : GB $ : $$\begin{align*} \frac{DG}{GB}.\frac{BE}{EA}.\frac{AC}{CD} &= 1\\\frac{DG}{GB}.\frac{2}{1}.\frac{4}{1} &= 1\\\frac{DG}{GB}.\frac{8}{1}&= 1\\\frac{DG}{GB} &= 1 : \frac{8}{1}\\\frac{DG}{GB} &= \frac{1}{8} \end{align*}$$

Bagaimana hasilnya? yups sama dengan menggunakan dalil menelaus.

Latihan 5

1. Diketahui titik P(1, 7) dan Q(4, 1). Titik R adalah sebuah titik pada garis hubung PQ, sehingga $\overset{\to }{\mathop{PR}}=\frac{1}{3}\overset{\to }{\mathop{PQ}}$. Tentukan koordinat titik R.