kali ini akan di bahas Rumus Jumlah Dan Selisih Dua Sudut pada Trigonometri yaitu Tangen beserta bukti dan contoh soal
Daftar Isi
Kali ini akan di membahas Rumus Jumlah Dan Selisih Dua Sudut pada Trigonometri yaitu Tangen beserta bukti dan contoh soalnya. Untuk tangen kita hanya perlu hapal atau memahami rumus-rumus sebelumnya saja. Materi ini adalah bagian lanjutan dari materi sebelumnya tentang Rumus Jumlah Dan Selisih sudut pada Sinus↝ .
3. Rumus untuk $\tan(\alpha+\beta)$ dan $\tan(\alpha-\beta)$
Rumus Jumlah dan Selisih dua sudut untuk tangen
$$ \begin{align*} \tan ( \alpha + \beta ) & = \frac{\tan \alpha + \tan \beta}{1 - \tan \alpha \tan \beta } \\ \tan ( \alpha - \beta ) & = \frac{\tan \alpha - \tan \beta}{1 + \tan \alpha \tan \beta } \end{align*}$$
Untuk membuktikan rumus $\tan(\alpha+\beta)$ dan $\tan(\alpha-\beta)$ diatas kita gunakan rumus trigonometri jumlah dua sudut $cos(\alpha+\beta)$ dan $cos(\alpha+\beta)$. Selain itu, kita juga menggunakan rumus identitas trigonometri $\tan A=\dfrac{\sin A}{\cos B}$.
Bukti rumus $ \tan ( \alpha + \beta ) = \dfrac{\tan \alpha + \tan \beta}{1 - \tan \alpha \tan \beta } $
$$\begin{align*} \tan ( \alpha + \beta ) & = \frac{ \sin ( \alpha + \beta ) }{\cos ( \alpha + \beta )} \\ & = \frac{\sin \alpha \cos \beta + \cos \alpha \sin \beta}{\cos \alpha \cos \beta - \sin \alpha \sin \beta} \\ & = \frac{\sin \alpha \cos \beta + \cos \alpha \sin \beta}{\cos \alpha \cos \beta - \sin \alpha \sin \beta} . \frac{\frac{1}{\cos \alpha \cos \beta}}{\frac{1}{\cos \alpha \cos \beta}} \\ & = \frac{\frac{\sin \alpha \cos \beta + \cos \alpha \sin \beta}{\cos \alpha \cos \beta}}{\frac{\cos \alpha \cos \beta - \sin \alpha \sin \beta}{\cos \alpha \cos \beta}} \\ & = \frac{\frac{\sin \alpha \cos \beta }{\cos \alpha \cos \beta} + \frac{\cos \alpha \sin \beta}{\cos \alpha \cos \beta}}{\frac{ \cos \alpha \cos \beta}{\cos \alpha \cos \beta} - \frac{ \sin \alpha \sin \beta}{\cos \alpha \cos \beta}} \\ & = \frac{\frac{\sin \alpha }{\cos \alpha } + \frac{ \sin \beta}{ \cos \beta}}{1 - \frac{ \sin \alpha }{\cos \alpha }\frac{ \sin \beta}{ \cos \beta}} \\ \tan ( \alpha + \beta ) & = \frac{ \tan \alpha + \tan \beta}{1 - \tan \alpha \tan \beta } \end{align*} $$
Terbukti bahwa $ \tan ( \alpha + \beta ) = \dfrac{\tan \alpha + \tan \beta}{1 - \tan \alpha \tan \beta } $
Bukti rumus $ \tan ( \alpha - \beta ) = \dfrac{\tan \alpha - \tan \beta}{1 + \tan \alpha \tan \beta } $
Untuk membuktikannya kita gunakan sudut berelasi di kuadran IV atau sudut negatif. Ingat bahwa $\tan (-A)=-\tan A$. $$\begin{align*} \tan ( \alpha - \beta ) & = \tan ( \alpha + (- \beta )) \\ & = \frac{ \tan \alpha + \tan (-\beta )}{1 - \tan \alpha \tan (-\beta ) } \\ & = \frac{ \tan \alpha - \tan \beta }{1 - \tan \alpha . (- \tan \beta ) } \\ & = \frac{ \tan \alpha - \tan \beta }{1 + \tan \alpha \tan \beta } \end{align*} $$
Contoh Soal Trigonometri Jumlah dan Selisih Dua Sudut Tangen
1). Tanpa menggunakan kalkulator dan tabel trigonometri. Tentukan nilai dari $\tan 75^\circ$!
Alternatif Penyelesaian
Gunakan rumus $\tan (a+b) = \dfrac{\tan a + \tan b}{1-\tan a. \tan b}$.
$$\begin{align*} \tan 75^\circ & = \tan ( 45^\circ + 30^\circ ) \\ & = \frac{ \tan 45^\circ + \tan 30^\circ}{1 - \tan 45^\circ \tan 30^\circ } \\ & = \frac{ 1 + \frac{1}{3} \sqrt{3} }{1 - 1.\frac{1}{3} \sqrt{3} } \\ & = \frac{ 1 + \frac{1}{3} \sqrt{3} }{1 - \frac{1}{3} \sqrt{3} } \times \frac{3}{3} \\ & = \frac{ 3 + \sqrt{3} }{3 - \sqrt{3} } \\ & = \frac{ 3 + \sqrt{3} }{3 - \sqrt{3} } \times \frac{ 3 + \sqrt{3} }{3 + \sqrt{3} } \\ & = \frac{ 9 + 6\sqrt{3} + 3 }{9 - 3 }\\& = \frac{ 12 + 6\sqrt{3} }{6 }\\ \tan 75^\circ & = 2 + \sqrt{3} \end{align*} $$
Jadi, nilai dari $\tan 75^\circ= 2+\sqrt{3}$.
2). Tentukan nilai dari $\tan 255^\circ$
Alternatif Penyelesaian
Gunakan rumus $\tan (a-b) = \dfrac{\tan a - \tan b}{1+\tan a. \tan b}$.
$$\begin{align*} \tan 255^\circ &= \tan(300^\circ-45^\circ)\\ &= \frac{\tan 300^\circ - \tan 45^\circ}{1+\tan 300^\circ \tan 45^\circ}\\ &= \frac{-\tan 60^\circ - \tan 45^\circ}{1-\tan 60^\circ \tan 45^\circ}\\ &= \frac{-\sqrt{3} - 1}{1-\sqrt{3} \cdot 1}\\ &= \frac{-\sqrt{3}-1}{-\sqrt{3}+1}\times \frac{-1}{-1}\\ &= \frac{\sqrt{3}+1}{\sqrt{3}-1}\times \frac{\sqrt{3}+1}{\sqrt{3}+1}\\ &= \frac{3+2\sqrt{3}+1}{3-1}\\ &= \frac{4+2\sqrt{3}}{2}\\ &= 2+\sqrt{3} \end{align*} $$
Jadi, nilai dari $\tan 255^\circ= 2+\sqrt{3}$.
3). Diketahui Diketahui $\sin p =\dfrac35$ dan $\cos q = \dfrac{12}{13}$ ($p$ di kuadran I dan $q$ di kuadran IV). Tentukan nilai dari $\tan(p+q)$!
Alternatif Penyelesaian
Gunakan rumus $\tan (a+b) = \dfrac{\tan a+\tan b}{1-\tan a. \tan b}$.
sin $p$ dan cos $q$ telah diketahui, sehingga kita perlu menentukan $\tan p$ dan $\tan q$ terlebih dahulu dengan menggambar segitiga saja.
Ingat perbandingan trigonometri
$\sin p =\dfrac{depan}{miring}=\dfrac{de}{mi}$
$\cos p =\dfrac{samping}{miring}=\dfrac{sa}{mi}$
$\tan p =\dfrac{depan}{samping}=\dfrac{de}{sa}$
Untuk $\sin p =\dfrac35=\dfrac{de}{mi}$ maka depan 3 miring 5 dan nilai $\tan p$ positif karena di kuadran I.
Untuk $\cos p =\dfrac{12}{13}=\dfrac{sa}{mi}$ maka depan 3 miring 5 dan nilai $\tan q$ negatif karena di kuadran IV.
Lihat gambar!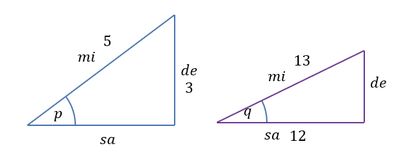
*) cari nilai $\tan p$ namun sebelumnya kita perlu mencari panjang samping dari segitiga dengan sudut $p$ dengan pythagoras.
$$sa=\sqrt{5^2-3^2}=\sqrt{25-9}=\sqrt{16}=4$$ Sehingga nilai dari $\tan p=\dfrac{de}{sa}=\dfrac{3}{4}$.
*) cari nilai $\tan q$ namun sebelumnya kita perlu mencari panjang samping dari segitiga dengan sudut $q$ dengan pythagoras.
$$de=\sqrt{13^2-12^2}=\sqrt{169-144}=\sqrt{25}=5$$ Sehingga nilai dari $\tan q=-\dfrac{de}{sa}=-\dfrac{5}{12}$ (negatif karena di kuadran IV).
*) cari nilai $\tan (p+q)$.
$$\begin{align*} \tan (p+q) &= \frac{\tan p+\tan q}{1-\tan p. \tan q}\\ &=\frac{\frac{3}{4}+\left(-\frac{5}{12}\right)}{1-\frac{3}{4}.\left(-\frac{5}{12}\right)}\\ &=\frac{\frac{3}{4}-\frac{5}{12}}{1+\frac{15}{48}}\\ &=\frac{\frac{36}{48}-\frac{20}{48}}{\frac{48}{48}+\frac{15}{48}}\\ &=\frac{\frac{16}{48}}{\frac{63}{48}}\\ &=\frac{16}{63} \end{align*}$$ Jadi, nilai dari $\tan(p+q)=\dfrac{16}{63}$
