Pelajari penerapan konsep bilangan berpangkat dalam kehidupan nyata, mulai dari pertumbuhan populasi, bunga majemuk, hingga teknologi digital. Dilengkapi dengan contoh soal dan pembahasan.
Daftar Isi
🔍 Mengapa Bilangan Berpangkat Penting di Kehidupan Nyata?
Bilangan berpangkat tidak hanya digunakan dalam pelajaran matematika, tetapi juga muncul di banyak bidang kehidupan nyata, antara lain:
- 📈 Pertumbuhan eksponensial (populasi, bakteri)
- 💰 Bunga majemuk di dunia perbankan
- 🔬 Peluruhan radioaktif dalam sains
- 🧮 Skala ukuran di dunia digital (byte, kilobyte, gigabyte)
- 🌍 Notasi ilmiah untuk menyederhanakan angka besar/kecil
🧪 Contoh Penerapan Bilangan Berpangkat
1. 📊 Pertumbuhan Populasi (Eksponensial)
Jika suatu populasi bertambah dua kali lipat setiap periode waktu tertentu, maka digunakan rumus:
$$ P = P_0 \cdot r^t $$
di mana:
- $P_0$ = populasi awal
- $r$ = rasio pertumbuhan
- $t$ = waktu
- $P$ = populasi akhir
Contoh: Sebuah bakteri berjumlah 100 berkembang biak dua kali lipat setiap 3 jam. Berapa jumlahnya setelah 12 jam?
$$ P = 100 \cdot 2^{12/3} = 100 \cdot 2^4 = 100 \cdot 16 = 1600 $$
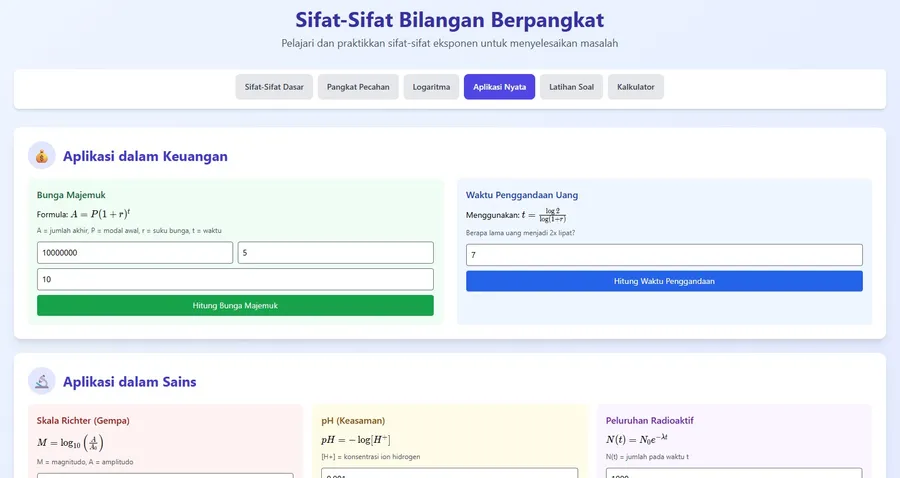
2. 💰 Bunga Majemuk (Compound Interest)
Dalam keuangan, rumus bunga majemuk:
$$ A = P \cdot (1 + r)^t $$
- $A$ = jumlah akhir
- $P$ = modal awal
- $r$ = suku bunga per periode
- $t$ = jumlah periode
Contoh: Uang Rp1.000.000 ditabung dengan bunga majemuk 5% per tahun selama 3 tahun:
$$ A = 1.000.000 \cdot (1 + 0{,}05)^3 = 1.000.000 \cdot 1{,}157625 = Rp1.157.625 $$
3. 🧬 Peluruhan Radioaktif
Peluruhan radioaktif digambarkan dengan:
$$ N = N_0 \cdot \left(\frac{1}{2}\right)^{t/h} $$
- $N_0$ = jumlah awal
- $t$ = waktu
- $h$ = waktu paruh
Contoh: Jika zat radioaktif memiliki waktu paruh 10 tahun dan massa awal 200 gram, berapa sisa massa setelah 30 tahun?
$$ N = 200 \cdot \left( \frac{1}{2} \right)^{30/10} = 200 \cdot \left( \frac{1}{2} \right)^3 = 200 \cdot \frac{1}{8} = 25 \text{ gram} $$
4. 💻 Teknologi Digital (Basis 2)
Dalam komputer:
- 1 kilobyte = $2^{10} = 1024$ byte
- 1 megabyte = $2^{20}$ byte
- 1 gigabyte = $2^{30}$ byte
🧠 Contoh Soal dan Pembahasan
Berapa byte dalam 1 kilobyte?
Alternatif Penyelesaian ✍️
$$ 2^{10} = 1024 \text{ byte} $$
Apa bentuk eksponen dari 1 gigabyte?
Alternatif Penyelesaian ✍️
$$ 2^{30} \text{ byte} $$
Jelaskan mengapa populasi yang bertumbuh secara eksponensial dapat dinyatakan dengan bilangan berpangkat.
Alternatif Penyelesaian ✍️
Karena setiap periode waktu populasi bertambah secara lipat, bukan hanya bertambah tetap. Ini sesuai dengan pola perkalian berulang yang direpresentasikan oleh eksponen.Mengapa bunga majemuk menghasilkan nilai lebih besar dibanding bunga tunggal?
Alternatif Penyelesaian ✍️
Karena bunga majemuk menghitung bunga atas bunga yang sudah diperoleh sebelumnya, mengikuti pola pertumbuhan eksponensial.Sebuah virus berkembang biak dua kali lipat setiap 6 jam. Jika awalnya ada 200 virus, berapa banyak setelah 1 hari?
Alternatif Penyelesaian ✍️
$$ t = \frac{24}{6} = 4,\quad V = 200 \cdot 2^4 = 200 \cdot 16 = 3200 $$
Berapa jumlah uang akhir dari tabungan Rp2.000.000 dengan bunga majemuk 10% per tahun selama 2 tahun?
Alternatif Penyelesaian ✍️
$$ A = 2.000.000 \cdot (1 + 0{,}10)^2 = 2.000.000 \cdot 1{,}21 = Rp2.420.000 $$
Sebuah zat radioaktif tinggal 12,5 gram dari 100 gram setelah beberapa tahun. Waktu paruhnya 5 tahun. Berapa lama waktu yang telah berlalu?
Alternatif Penyelesaian ✍️
$$ \frac{1}{8} \cdot 100 = 12{,}5 \Rightarrow \left( \frac{1}{2} \right)^3 = \frac{1}{8} \Rightarrow t = 3 \cdot 5 = 15 \text{ tahun} $$
Seorang siswa membeli harddisk 1 TB. Berapa byte total kapasitasnya dalam bentuk eksponen?
Alternatif Penyelesaian ✍️
1 TB = $2^{40}$ byte = 1.099.511.627.776 byte
🎯 Kesimpulan
Bilangan berpangkat sangat berguna dalam kehidupan nyata, mulai dari penghitungan ekonomi, ilmu sains, hingga teknologi digital. Memahami penerapannya membantu siswa melihat relevansi nyata matematika dalam dunia sehari-hari.
ingin belajar yang lebih interaktif buka media pembelajaran berikut Media Pembelajaran Bilangan Berpangkat↝