Matematika SMP Fase D: Faktorisasi Prima & Rasio

Pelajari Materi faktorisasi prima dan rasio: skala, proporsi, serta laju perubahan. Disertai contoh dan soal sehari-hari. Cocok untuk kelas VII, VIII, dan IX.

Faktorisasi Prima dan Rasio dalam Kehidupan Sehari-hari

Matematika bukan hanya sekadar hitung-hitungan di atas kertas. Setiap hari, tanpa kita sadari, kita sering menggunakan konsep matematika untuk membuat keputusan dan memecahkan masalah. Misalnya, saat kamu ingin membagi kue secara adil dengan temanmu, menentukan rute tercepat ke sekolah, membaca denah lokasi, atau membandingkan harga barang di toko. Semua itu berkaitan dengan rasio, proporsi, dan bahkan faktorisasi prima.

Di fase ini, kamu akan belajar bagaimana:

• Bilangan bisa dipecah ke dalam bentuk lebih sederhana melalui faktorisasi prima.
• Perbandingan dan rasio digunakan untuk membandingkan dua nilai.
• Skala membantu kita memahami ukuran peta atau denah.
• Proporsi membantu menghitung secara adil dan efisien.
• Laju perubahan berguna untuk menghitung kecepatan, efisiensi, atau pertumbuhan suatu nilai terhadap waktu.

Mempelajari semua ini bukan hanya untuk mengerjakan soal ujian, tetapi juga agar kamu siap menghadapi tantangan dalam kehidupan sehari-hari dengan cara yang lebih cerdas dan logis.

Capaian Pembelajaran

Peserta didik dapat menggunakan faktorisasi prima dan pengertian rasio (skala, proporsi, dan laju perubahan) dalam penyelesaian masalah.

🎯 Tujuan Pembelajaran

Setelah mempelajari materi ini, peserta didik dapat:

• Melakukan faktorisasi prima untuk bilangan bulat.
• Menggunakan rasio, skala, proporsi, dan laju perubahan dalam menyelesaikan masalah sehari-hari.

1. 🧩 Faktorisasi Prima

🔍 Apa itu Faktorisasi Prima?

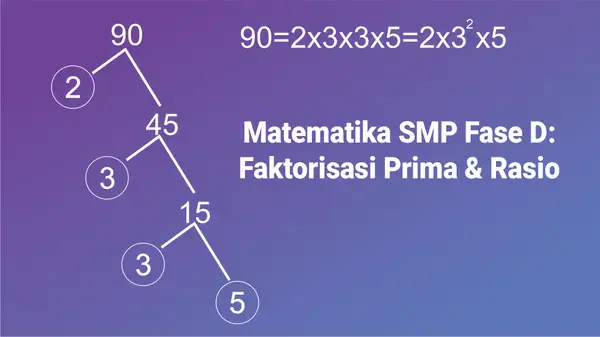
Faktorisasi prima adalah proses memecah bilangan menjadi perkalian faktor-faktor bilangan prima.

Contoh bilangan prima: 2, 3, 5, 7, 11, 13, 17, …

✍️ Contoh:

Faktorkan 90 ke dalam bentuk prima.

$$90 = 2 \times 3 \times 3 \times 5 = 2 \times 3^2 \times 5$$

💡 Kegunaan:

• Menyederhanakan pecahan
• Menentukan FPB (Faktor Persekutuan Terbesar) & KPK (Kelipatan Persekutuan Terkecil)

2. ⚖️ Rasio

🔍 Apa itu Rasio?

Rasio adalah perbandingan antara dua nilai. Biasanya ditulis dalam bentuk pecahan atau “a : b”.

✍️ Contoh:

Jika jumlah siswa laki-laki dan perempuan di kelas adalah 12 dan 16, maka rasio laki-laki : perempuan:

$$\frac{12}{16} = \frac{3}{4} \Rightarrow 3 : 4$$

3. 🗺️ Skala

🔍 Apa itu Skala?

Skala menyatakan perbandingan ukuran gambar (misalnya peta atau denah) dengan ukuran sebenarnya.

$$\text{Skala} = \frac{\text{Ukuran gambar}}{\text{Ukuran sebenarnya}}$$

✍️ Contoh:

Jika 1 cm pada peta mewakili 5 km di dunia nyata, maka skalanya adalah:

$$1 : 500.000 \quad (\text{karena 5 km} = 500.000 \text{ cm})$$

4. ⚖️ Proporsi

🔍 Apa itu Proporsi?

Proporsi adalah dua rasio yang nilainya sama.

$$\frac{a}{b} = \frac{c}{d}$$

✍️ Contoh:

Jika 2 pensil harganya Rp6.000, maka 5 pensil harganya?

$$\frac{2}{6000} = \frac{5}{x} \Rightarrow 2x = 5 \times 6000 = 30.000 \Rightarrow x = 15.000$$

5. 🏃‍♂️ Laju Perubahan

🔍 Apa itu Laju Perubahan?

Laju perubahan menunjukkan seberapa cepat suatu nilai berubah terhadap waktu atau jarak.

$$\text{Laju} = \frac{\text{Jarak}}{\text{Waktu}}$$

✍️ Contoh:

Sebuah mobil menempuh 150 km dalam waktu 3 jam. Maka:

$$\text{Laju} = \frac{150}{3} = 50 \text{ km/jam}$$

🧠 Soal Latihan

1. Faktorkan 72 ke dalam bentuk faktorisasi prima.
2. Jika skala peta adalah 1 : 100.000, maka jarak 6 cm di peta mewakili berapa km?
3. Jika 3 buku harganya Rp45.000, berapa harga 7 buku?
4. Seseorang berjalan 2,5 km dalam 30 menit. Berapa laju jalannya dalam km/jam?

🧠 Contoh Soal Kehidupan Sehari-hari

Andi menggambar denah rumah dengan skala 1 : 200. Jika panjang ruang tamu di gambar adalah 3 cm, berapa panjang sebenarnya dalam meter?

$$3 \text{ cm} \times 200 = 600 \text{ cm} = 6 \text{ meter}$$

📌 Kesimpulan

Konsep faktorisasi prima dan rasio sangat penting dalam kehidupan sehari-hari. Dari menyederhanakan pecahan, membaca peta, menghitung harga, hingga memahami kecepatan, semua membutuhkan kemampuan matematika dasar ini.