Pelajari rumus dan contoh soal perbandingan trigonometri (sin, cos, tan) pada segitiga siku-siku sudut lancip. Lengkap dengan pembahasan dan soal HOTS!
Daftar Isi
Trigonometri itu dimulai dari segitiga siku-siku. Dari sini kita belajar hubungan antara sisi-sisi segitiga dan sudutnya, yang disebut perbandingan trigonometri. Ada tiga yang utama: sinus (sin), cosinus (cos), dan tangen (tan). Trigonometri berasal dari dua kata Yunani: trigonon (tiga sudut) dan metron (pengukuran). Dalam matematika, kita mengenal trigonometri melalui segitiga siku-siku. Di sinilah kita mulai mengenal perbandingan sisi-sisi dalam segitiga terhadap sudut, yaitu sinus (sin), cosinus (cos), dan tangen (tan). Dalam artikel ini, kamu akan mempelajari secara menyeluruh bagaimana menentukan nilai perbandingan trigonometri pada segitiga siku-siku, lengkap dengan contoh soal, pembahasan, latihan, dan soal HOTS.
🧠 Konsep Dasar
Perbandingan trigonometri adalah perbandingan antara panjang sisi-sisi segitiga siku-siku yang digunakan untuk menentukan hubungan sudut terhadap sisi.
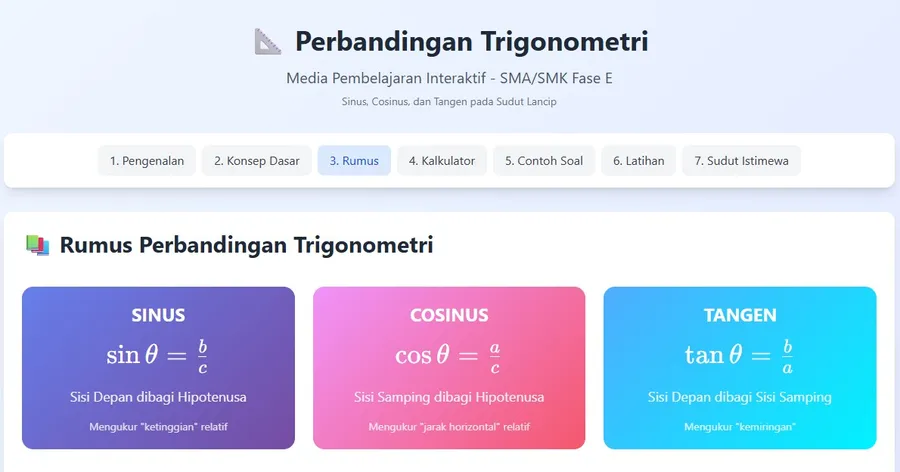
Dalam segitiga siku-siku, dikenal 3 fungsi utama:
- Sinus (sin): perbandingan sisi di depan sudut terhadap sisi miring.
- Cosinus (cos): perbandingan sisi samping terhadap sisi miring.
- Tangen (tan): perbandingan sisi di depan sudut terhadap sisi samping.
Misalkan segitiga ABC dengan sudut siku-siku di C.
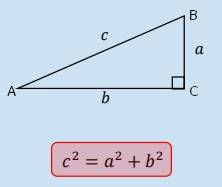
Jika:
- $\angle A$ adalah sudut lancip
- $a = BC$ (sisi depan sudut A)
- $b = AC$ (sisi samping sudut A)
- $c = AB$ (sisi miring)
Maka:
$$ \sin A = \frac{a}{c}, \quad \cos A = \frac{b}{c}, \quad \tan A = \frac{a}{b} $$
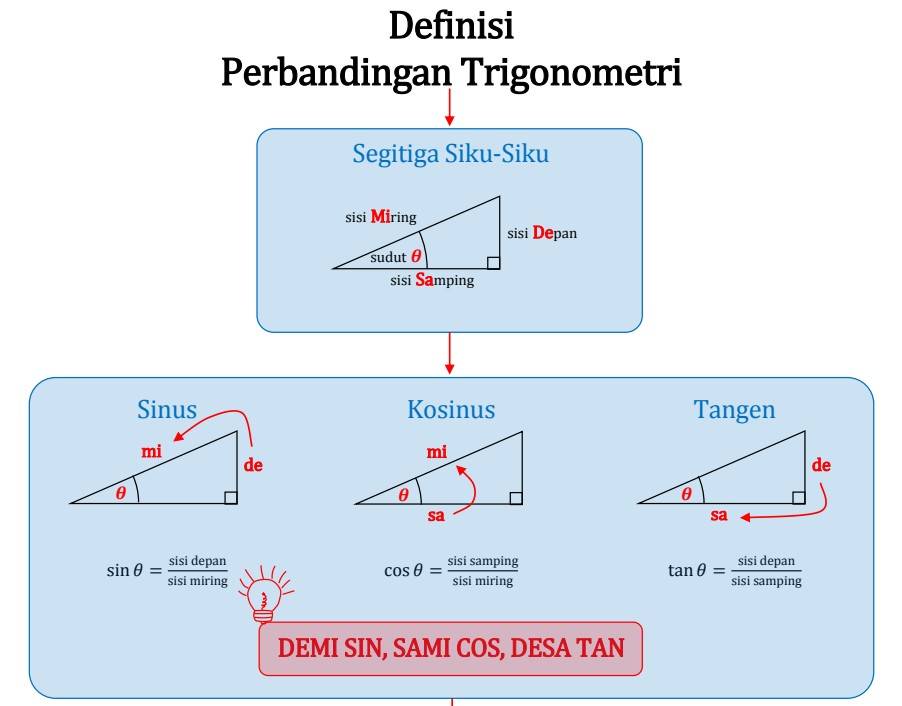
Cara Menghafal Rumus Trigonometri
🧠 Cara Mudah menghafal sin cos tan Gunakan trik “SINDEMI - COSAMI - TANDESA” sebagai singkatan:
🧪 Contoh Soal Trigonometri dan Pembahasan
✅ Contoh Soal 1
Sebuah segitiga siku-siku memiliki sisi depan sudut A = 6 cm dan sisi miring = 10 cm. Hitung nilai:
- $\sin A$
- $\cos A$
- $\tan A$
Alternatif Penyelesaian ✍️
Diketahui $a = 6$, $c = 10$
Gunakan Teorema Pythagoras:
$$ b = \sqrt{10^2 - 6^2} = \sqrt{100 - 36} = \sqrt{64} = 8 $$
Maka:
- $\sin A = \frac{6}{10} = 0{,}6$
- $\cos A = \frac{8}{10} = 0{,}8$
- $\tan A = \frac{6}{8} = 0{,}75$
✅ Contoh Soal 2
Tuliskan rumus trigonometri sinus, cosinus, dan tangen pada segitiga siku-siku!
Alternatif Penyelesaian ✍️
- $\sin \theta = \frac{\text{sisi depan}}{\text{sisi miring}}$
- $\cos \theta = \frac{\text{sisi samping}}{\text{sisi miring}}$
- $\tan \theta = \frac{\text{sisi depan}}{\text{sisi samping}}$
✅ Contoh Soal 3
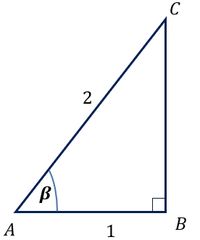
Diketahui $\cos \beta^\circ = \frac{1}{2}$ dan $\beta$ sudut lancip ($0^\circ < \beta < 90^\circ$). Carilah nilai perbandingan trigonometri sudut $\beta$ yang lain.
Alternatif Penyelesaian ✍️
- identifikasi sisi segitiga
$\cos \beta^\circ = \frac{1}{2}=\frac{sa}{mi}$, kita dapatkan panjang sisi samping 1 dan panjang sisi miring 2 - menggambar segitiga siku-siku, misalkan $\triangle ABC$ siku-siku di B dan $\angle BAC = \beta$ maka AB=1 dan AC=2
Perhatikan gambar berikut
- mencari panjang sisi AB atau sisi depan dengan pythagoras.
$$\begin{align*} BC&=\sqrt{AC^2-AB^2}\\ &=\sqrt{2^2-1^2}\\ &=\sqrt{4-1}\\ BC&=\sqrt{3}\end{align*}$$ - mencari nilai $\sin\beta, \cos\beta, \tan\beta$ $$\sin\beta=\frac{de}{mi}=\frac{BC}{AC}=\frac{\sqrt{3}}{2}=\frac{1}{2}\sqrt{3}$$ $$\cos\beta=\frac{sa}{mi}=\frac{AB}{AC}=\frac{1}{2}$$ $$\tan\beta=\frac{de}{sa}=\frac{BC}{AB}=\frac{\sqrt{3}}{1}=\sqrt{3}$$
✅ Contoh Soal 4
Diketahui panjang sisi depan sudut A = 6 cm, sisi samping = 8 cm. Hitung nilai:
- Sisi miring
- $\sin A$, $\cos A$, dan $\tan A$
Alternatif Penyelesaian ✍️
- Gunakan Pythagoras:
$$ c = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10 $$
Trigonometri:
- $\sin A = \frac{6}{10} = 0{,}6$
- $\cos A = \frac{8}{10} = 0{,}8$
- $\tan A = \frac{6}{8} = 0{,}75$
✅ Contoh Soal 5
Sebuah tiang bendera setinggi 8 meter membentuk sudut elevasi 60° jika dilihat dari titik A di tanah. Berapa jarak mendatar titik A ke dasar tiang? Gunakan $\tan 60^\circ = \sqrt{3}$
Alternatif Penyelesaian ✍️
Gunakan rumus:
$$ \tan \theta = \frac{\text{tinggi}}{\text{jarak}} \Rightarrow \sqrt{3} = \frac{8}{x} \Rightarrow x = \frac{8}{\sqrt{3}} \approx 4{,}62 \text{ meter} $$
✅ Contoh Soal 6
Seorang siswa menghitung bahwa perosotan sepanjang 6 meter dengan kemiringan 30° memiliki tinggi 4 meter. Apakah perhitungan siswa tersebut benar? Gunakan $\sin 30^\circ = 0{,}5$
Alternatif Penyelesaian ✍️
Gunakan $\sin \theta = \frac{\text{tinggi}}{\text{miring}} = \frac{4}{6} \approx 0{,}666$, sedangkan $\sin 30^\circ = 0{,}5$. Kesimpulan: Perhitungan siswa salah, karena seharusnya tinggi = $0{,}5 \times 6 = 3$ meter.
✅ Contoh Soal 7
Sebuah papan seluncur dipasang dengan sudut 45° dan panjang 4 meter. Tentukan tinggi papan dari tanah.
Alternatif Penyelesaian ✍️
Gunakan $\sin 45^\circ = \frac{\text{tinggi}}{4} \Rightarrow \text{tinggi} = 4 \times \frac{\sqrt{2}}{2} = 2\sqrt{2} \approx 2{,}83$ meter🎯 Soal Latihan Mandiri
Diketahui segitiga siku-siku dengan panjang sisi depan = 9 cm, sisi samping = 12 cm. Hitung:
- a. Sisi miring
- b. Nilai sin, cos, dan tan
Sebuah tangga 5 m disandarkan ke tembok dengan sudut kemiringan 53°. Jika $\sin 53^\circ = 0{,}8$, tentukan tinggi tembok.
🔥 Soal HOTS
Seorang pekerja bangunan ingin memasang tiang penyangga pada sudut kemiringan 60°. Jika panjang tiang 3 meter, berapa jarak alas tiang ke tembok?
Petunjuk: gunakan $\cos \theta = \frac{\text{samping}}{\text{miring}}$
Di sebuah taman bermain, perosotan memiliki panjang 4 meter dan sudut kemiringan 45°. Hitung ketinggian dari tanah ke atas perosotan. Gunakan nilai $\sin 45^\circ = \frac{\sqrt{2}}{2} \approx 0{,}707$
📝 Kesimpulan
Perbandingan trigonometri sangat penting sebagai dasar dari semua materi trigonometri lainnya. Pemahaman sin, cos, dan tan dari segitiga siku-siku akan menjadi fondasi kuat untuk melanjutkan ke topik sudut berelasi, koordinat, grafik fungsi, dan lainnya.