Fungsi invers merupakan fungsi kebalikan yang dipelajari pada fase F kelas XI, simak pengertian, rumus, contoh penjelasannya disini!
Sobat Sinmat, pernahkah kamu mendengar kata antonim atau kebalikan? Misalnya, senang kebalikannya sedih, positif kebalikannya negatif dan lain-lain. Ternyata dalam matematika juga ada istilah kebalikan lho, khususnya pada fungsi, fungsi kebalikan tersebut biasa dikenal dengan nama fungsi invers. Lalu, apakah fungsi invers itu? Simak penjelasan di bawah ini ya!
Pengertian Fungsi Invers
 Fungsi invers atau fungsi kebalikan merupakan suatu fungsi yang berkebalikan dari fungsi asalnya. Suatu fungsi f memiliki fungsi invers (kebalikan) f−1 jika f merupakan fungsi satu-satu dan fungsi pada (bijektif). Hubungan tersebut dapat dinyatakan sebagai berikut:
Fungsi invers atau fungsi kebalikan merupakan suatu fungsi yang berkebalikan dari fungsi asalnya. Suatu fungsi f memiliki fungsi invers (kebalikan) f−1 jika f merupakan fungsi satu-satu dan fungsi pada (bijektif). Hubungan tersebut dapat dinyatakan sebagai berikut:
(f−1)−1=f
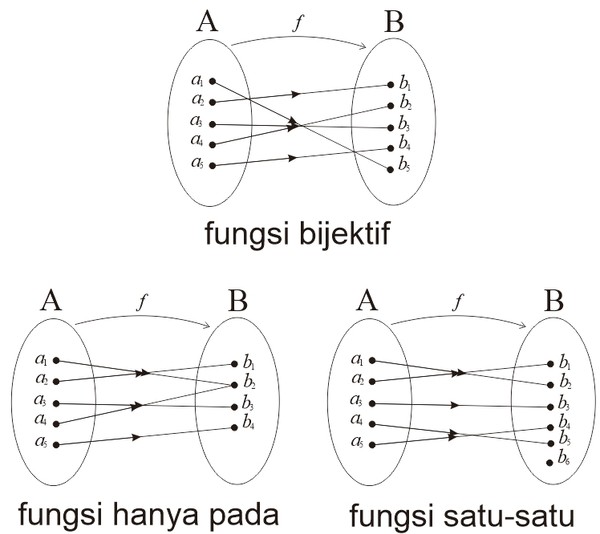
Sederhananya, fungsi bijektif terjadi ketika jumlah anggota domain sama dengan jumlah anggota kodomain. Tidak ada dua atau lebih doamain berbeda dipetakan ke kodomain yang sama dan setiap kodomain memiliki pasangan di domain, perhatikan gambar di bawah ini:

Berdasarkan gambar pemetaan di atas, pemetaan pertama merupakan fungsi bijektif. Pemetaan kedua bukan fungsi bijektif karena pemetaan tersebut hanya terjadi fungsi pada. Domain a4 dan a1 dipetakan ke anggota kodomain yang sama. Pemetaan ketiga bukan fungsi bijektif karena pemetaan tersebut hanya terjadi fungsi satu-satu. Kodomain b6 tidak memiliki pasangan pada anggota domain.
Definisi Fungsi Invers
Jika fungsi
f memetakan A ke B dan dinyatakan dalam pasangan berurutan
f={(x,y)∣x∈A dan y∈B}, maka invers fungsi
f (dilambangkan
f−1) adalah relasi yang memetakan B ke A, dalam pasangan berurutan dinyatakan dengan
f−1={(y,x)∣y∈B dan x∈A}.
Dapat ditulis: jika
y=f(x) maka inversnya
x=f−1(y)Cara menentukan fungsi invers dari fungsi awalnya
Ada 3 langkah untuk menentukan fungsi invers, yaitu:
- Buatlah permisalan f(x)=y pada persamaan.
- Selesaikan persamaan sehingga diperoleh x sebagai fungsi y atau x=f−1(y).
- Ubah variabel y dengan x pada f−1(y) sehingga diperoleh f−1(x)=y sebagai fungsi invers dari y=f(x).
Supaya kamu lebih jelas dan paham, coba kita kerjakan contoh soal ini ya.
Contoh Soal Fungsi Invers
Jika diketahui f(x)=2x+3 tentukan inversnya dan nilai f−1(1) !
Alternatif Penyelesaian ✍️
Misalkan f(x)=y dan rubahlah kedalam bentuk x=f−1(y)
f(x)2x+32xxberdasarkan xdiperoleh f−1(y)=y=y=y−3=2y−3=f−1(y)=2y−3
Gantilah variabel y dengan x, artinya f−1(x)=2x−3
Jadi, invers dari fungsi f(x)=2x+3, adalah f−1(x)=2x−3
Menentukan nilai f−1(1)
f−1(x)=2x−3→f−1(1)=21−3=2−2=−1
Jadi, diperoleh nilai f−1(1)=−1
Diketahui fungsi g(x)=2x+53x−1 , tentukanlah inversnya.!
Alternatif Penyelesaian ✍️
Misalkan g(x)=y dan rubahlah kedalam bentuk x=g−1(y)g(x)yy(2x+5)2xy+5y2xy−3xx(2y−3)xberdasarkan xdiperoleh f−1(y)=2x+53x−1=2x+53x−1=3x−1=3x−1=−5y−1=−5y−1=2y−3−5y−1=f−1(y)=2y−3−5y−1
Gantilah variabel y dengan x, artinya f−1(x)=2x−3−5x−1
Jadi, invers dari fungsi f(x)=2x+53x−1, adalah f−1(x)=2x−3−5x−1
Cara lebih praktis : f(x)=cx+dax+b→f−1(x)=−cx+adx−b
g(x)=2x+53x−1→g−1(x)=−2x+35x+1
g−1(x)=−2x+35x+1×−1−1=2x−3−5x−1
Jadi, invers dari fungsi f(x)=2x+53x−1, adalah f−1(x)=2x−3−5x−1
Diketahui f(x)=5x−3. Jika f−1(a)=2, maka nilai a+5=….
Alternatif Penyelesaian ✍️
- Menentukan inversnya
f(x)y5xxf−1(x)f−1(a)=5x−3=5x−3=y+3=5y+3=5x+3=5a+3
- Menenukan nilai a
f−1(a)5a+3a+3a=2=2=10=7
Sehingga nilai a+5=7+5=12
Oke Sobat, sekarang kamu sudah paham ‘kan apakah fungsi invers itu? Fungsi invers ini adalah fungsi kebalikan dari fungsi asalnya. Agar kamu lebih paham, silakan kerjakan latihan soal dibawah ini
Latihan Soal Fungsi Invers
- Diketahui f(x)=x+25x−3,x=−2 dan g(x)=6x–2, tentukan:
- f−1(x)
- g−1(x)
- (f∘g)−1(x)
- (g∘f)−1(x)
- Diketahui f(x)=3x+2 dan (g∘f)(x)=6x−4. Tentukan
- g−1(x)
- Nilai g−1(2)
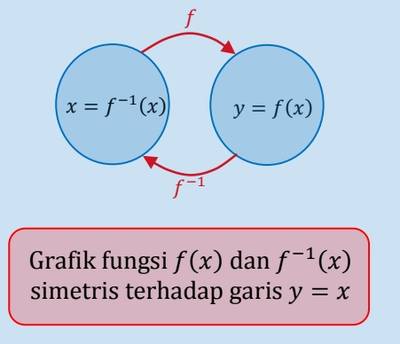 Fungsi invers atau fungsi kebalikan merupakan suatu fungsi yang berkebalikan dari fungsi asalnya. Suatu fungsi memiliki fungsi invers (kebalikan) jika merupakan fungsi satu-satu dan fungsi pada (bijektif). Hubungan tersebut dapat dinyatakan sebagai berikut:
Fungsi invers atau fungsi kebalikan merupakan suatu fungsi yang berkebalikan dari fungsi asalnya. Suatu fungsi memiliki fungsi invers (kebalikan) jika merupakan fungsi satu-satu dan fungsi pada (bijektif). Hubungan tersebut dapat dinyatakan sebagai berikut: