Ukuran Letak dari data memiliki konsep yang sama persis dengan median data. Ukuran letak data diantaranya kuartil, desil, dan persentil.
Ukuran Letak dari data memiliki konsep yang sama persis dengan median data. Ya!!!! Karena median adalah ukuran letak yang membagi data terurut menjadi dua bagian sama besar.
Sebelumnya kita sudah belajar tentang ukuran pemusatan data↝
dan juga Penyajian Data↝
, kali ini kita lanjutkan tentang ukuran letak data yang didasarkan pada letak ukuran tersebut dalam suatu distribusi data. Ukuran letak data membagi sekumpulan data yang berurutan menjadi beberapa bagian yang sama, diantaranya kuartil, desil, dan persentil.
Secara ringkas
- Median adalah ukuran letak yang membagi data menjadi 2 bagian yang sama besar.
- Kuartil adalah ukuran letak yang membagi data menjadi 4 bagian yang sama besar.
- Desil adalah ukuran letak yang membagi data menjadi 10 bagian yang sama besar.
- Persentil adalah ukuran letak yang membagi data menjadi 100 bagian yang sama besar.
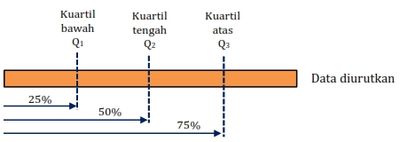
Kuartil
Kuartil adalah nilai pembatas yang membagi data terurut menjadi empat bagian yang sama.Kuartil terdiri dari tiga jenis yaitu kuartil pertama (Q1) yang disebut juga kuartil bawah, kuartil kedua (Q2) yang disebut juga median atau nilai tengah, dan kuartil ketiga (Q3) yang disebut juga kuartil atas. Gambarannya sebagai berikut.

Kuartil Data Tunggal
Kuartil data tunggal ditentukan dengan rumus:
Letak Qi= data ke-(4i(n+1)) atau Qi=X4i(n+1)
dengan i=1,2,3 dan n adalah banyak datum(banyak nilai).
Contoh:
Disajikan data nilai hasil penilaian matematika terhadap 20 siswa sebagai berikut
68, 68, 34, 68, 18, 52, 68, 50, 88, 68, 68, 32, 88, 32, 32, 68, 64, 90, 32, 88.
Tentukan nilai masing-masing kuartilnya!
Penyelesaian
Urutkan data terlebih dahulu
18, 32, 32, 32, 32, 34, 50, 52, 64, 68, 68, 68, 68, 68, 68, 68, 88, 88, 88, 90
Cari nilai quartil dengan mengetahui letaknya
 Kuartil 1 (Q1)
Kuartil 1 (Q1)
Letak Q1= data ke 41(n+1), sehingga
Letak Q1= data ke 41(20+1) = data ke 5,25
perhatikan bahwa nilai data ke 5,25 berarti data ke 5 lebih, 6 kurang sehingga terletak diantara nilai 32 dan 34.
Q1=32+0,25×(34−32)Q1=32+0,25×2Q1=32+0,5=32,5
Kuartil 2 (Q2)
Letak Q2= data ke 42(n+1), sehingga
Letak Q2= data ke 42(20+1) = data ke 10,5
perhatikan bahwa nilai data ke 10,5 berarti nilai diatntara data ke 10 dan 11 sehingga terletak diantara nilai 68 dan 68.
Q2=68+0,5×(68−68)Q2=68+0,8×0Q2=68
Kuartil 3 (Q3)
Letak Q3= data ke 43(n+1), sehingga
Letak Q3= data ke 43(20+1) = data ke 15,75
perhatikan bahwa nilai data ke 15,75 terletak diantara nilai 68 dan 68.
Q3=68+0,75×(68−68)Q3=68+0,75×0Q1=68
Kuartil Data Berkelompok
Langkah-langkah menentukan kuartil data berkelompok :
Tentukan letak kuartil (kelas kuartil) dengan rumus :
Letak Qi=data ke-4i(n+1)
dengan i=1,2,3 dan n adalah banyak datum(total frekuensi).
Hitung kuartil dengan rumus :
Qi=Tb+(fi4in−Fksi)p
Keterangan
Tb= tepi bawah kelas kuartil ke-i
Fksi= frekuensi kumulatif sebelum kelas kuartil ke-i
fi= frekuensi kelas kuatril ke-i
p= panjang kelas (lebar interval kelas)
i=1,2,3
Rumus panjang kelas :
p=(tepi atas − tepi bawah) atau
p=(batas atas − batas bawah+1)
Contoh
Tentukan Q1 dan Q3 data berat badan 50 orang siswa SMA Merdeka pada tabel berikut.
| Berat Badan | Frekuensi |
|---|
| 31–35 | 4 |
| 36–40 | 6 |
| 41–45 | 9 |
| 46–50 | 14 |
| 51–55 | 10 |
| 56–60 | 5 |
| 61–65 | 2 |
Alternatif Penyelesaian
Langkah awal kita tambahkan kolom Frekuensi Kumulatif (Fk).

Kuartil 1 (Q1)
Letak Q1 pada datum ke 41n=41(50)=12,5
Jadi, letak Q1 pada interval kelas : 41 – 45 (Frekuensi kumulatif 19, berarti letak data ke-11 sampai ke-19)
Tb=41–0,5=40,5
p=5,
Fks=10 dan fi=9
Sehingga diperoleh Kuartil bawah (Q1) adalah
Q1=Tb+(f41n−Fks)p=40,5+(941(50)−10)5=40,5+(912,5−10)5=40,5+(92,5)5=40,5+912,5=40,5+1,39=41,89
Jadi, nilai kuartil bawah (Q1) berat badan siswa SMA Merdeka adalah 41,89 kg.
Kuartil 3 (Q3)
Letak Q3 pada datum ke 43n=43(50)=37,5
Jadi, letak Q3 pada interval kelas : 51 – 55 (Frekuensi kumulatif 43, berarti letak data ke-34 sampai ke-43)
Tb=51–0,5=50,5
p=5,
Fks=33 dan fi=10
Sehingga diperoleh Kuartil bawah (Q3) adalah
Q3=Tb+(f43n−Fks)p=50,5+(1043(50)−33)5=50,5+(1037,5−33)5=50,5+(104,5)5=50,5+24,5=50,5+2,25=52,75
Jadi, nilai kuartil bawah (Q3) berat badan siswa SMA Merdeka adalah 52,75 kg.
Desil (Membagi 10 bagian sama besar dari data terurut)
Jika kumpulan data dibagi menjadi 10 bagian yang sama, maka didapat 9 pembagian dan tiap pembagian itu dinamakan desil
Desil Data Tunggal
Desil data tunggal ditentukan dengan rumus:
Letak Di atau Di= data ke-(10i(n+1))=X10i(n+1)
dengan i=1,2,3,…,9 dan n adalah banyak datum (banyak nilai).
Contoh:
Disajikan data nilai hasil penilaian matematika terhadap 20 siswa sebagai berikut
68, 68, 34, 68, 18, 52, 68, 50, 88, 68, 68, 32, 88, 32, 32, 68, 64, 90, 32, 88.
Tentukan nilai Desil ke-1 dan Desil ke-5!
Penyelesaian
Urutkan data terlebih dahulu
18, 32, 32, 32, 32, 34, 50, 52, 64, 68, 68, 68, 68, 68, 68, 68, 88, 88, 88, 90
Cari nilai Desil
Rumus : DiD1D5=X10i(n+1)=X101(20+1)=X2,1=x2+0,1(x3−x2)=32+0,1(32−32)=32+0,1(0)=32=X105(20+1)=X10,5=2x10+x11=268+68=68
Jadi, nilai desil ke-1 adalah 32 dan desil ke-5 adalah 68.
Desil Data Berkelompok
Langkah-langkah menentukan desil data berkelompok :
Tentukan letak desil (kelas desil) dengan rumus :
Letak Di=data ke-10i(n+1)
dengan i=1,2,3,…,9 dan n adalah banyak datum(total frekuensi).
Hitung desil dengan rumus :
Di=Tb+(fD10in−Fksi)p
Keterangan
Tb= tepi bawah kelas desil ke-i
Fksi= frekuensi kumulatif sebelum kelas desil ke-i
fD= frekuensi kelas kuatril ke-i
p= panjang kelas (lebar interval kelas)
i=1,2,3,…,9
Rumus panjang kelas :
p=(tepi atas − tepi bawah) atau
p=(batas atas − batas bawah+1)
Contoh
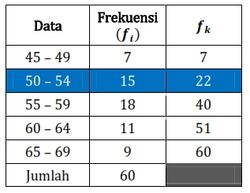
Tentukan D4 dari data usia 60 orang di Desa Merdeka pada tabel berikut.
| Data | Frekuensi |
|---|
| 45–49 | 7 |
| 50–54 | 15 |
| 55–59 | 18 |
| 60–64 | 11 |
| 65–69 | 9 |
Alternatif Penyelesaian
Langkah awal kita tambahkan kolom Frekuensi Kumulatif (Fk).

Desil 4 (D4)
Letak D4 pada datum ke 104n=104(60)=24
Jadi, letak D4 pada interval kelas : 55 – 59
Tb=55–0,5=54,5
p=5,
Fks=22 dan fD=18
Sehingga diperoleh desil ke-4 (D4) adalah
D4=Tb+(fD104n−Fks)p=54,5+(18104(60)−22)5=54,5+(1824−22)5=54,5+(182)5=54,5+0,56=55,06
Jadi, nilai desil ke-4 (D4) usia di Desa Merdeka adalah 50,06 kg.
Mudah bukan?! 😄
Persentil (Membagi 100 bagian sama besar dari data terurut)
Jika kumpulan data dibagi menjadi 100 bagian yang sama, maka didapat 99 pembagian dan tiap pembagian itu dinamakan Persentil. Persentil terdiri dari 99 jenis, yaitu persentil pertama (P1), persentil kedua (P2), dan seterusnya sampai persentil sembilan puluh sembilan (P99).
Persentil Data Tunggal
Persentil data tunggal ditentukan dengan rumus:
Letak Pi atau Pi= data ke-(100i(n+1))=X100i(n+1)
dengan i=1,2,3,…,99 dan n adalah banyak datum (banyak nilai).
Contoh:
Diketahui: 9, 10, 11, 6, 8, 7, 7, 5, 4, 5, tentukan persentil ke-30 dan persentil ke-75.
Penyelesaian :
Data diurutkan: 4, 5, 5, 6, 7, 7, 8, 9, 10, 11
ada 10 data (n=10)
- Letak persentil ke-30 dan nilainya :
PiP30=X100i(n+1)=X10030(10+1)=X3,3=x3+0,3(x4−x3)=5+0,3(6−5)=5+0,3=5,3 - Letak persentil ke-75 dan nilainya :
PiP75=X100i(n+1)=X10075(10+1)=X8,25=x8+0,25(x9−x8)=9+0,25(10−9)=9+0,25=9,25
Jadi, nilai persentil ke-30 adalah 5,3 dan desil ke-75 adalah 9,25.
Persentil Data Berkelompok
Langkah-langkah menentukan Persentil data berkelompok :
Tentukan letak Persentil (kelas Persentil) dengan rumus :
Letak Pi=data ke-100i(n+1)
dengan i=1,2,3,…,99 dan n adalah banyak datum(total frekuensi).
Hitung Persentil dengan rumus :
Pi=Tb+(fP100in−Fksi)p
Keterangan
Tb= tepi bawah kelas Persentil ke-i
Fksi= frekuensi kumulatif sebelum kelas Persentil ke-i
fP= frekuensi kelas kuatril ke-i
p= panjang kelas (lebar interval kelas)
i=1,2,3,…,99
Rumus panjang kelas :
p=(tepi atas − tepi bawah) atau
p=(batas atas − batas bawah+1)
Contoh
Tentukan P26 dari data usia 60 orang di Desa Merdeka pada tabel berikut.
| Data | Frekuensi |
|---|
| 45–49 | 7 |
| 50–54 | 15 |
| 55–59 | 18 |
| 60–64 | 11 |
| 65–69 | 9 |
Alternatif Penyelesaian
Langkah awal kita tambahkan kolom Frekuensi Kumulatif (Fk).

**Persentil 26 (P26)**
Letak P26 pada datum ke 10026n=10026(60)=15,6
Jadi, letak P26 pada interval kelas : 50 – 54
Tb=50–0,5=49,5
p=5,
Fks=7 dan fP=15
Sehingga diperoleh Persentil ke-26 (P26) adalah
P26=Tb+(fP10026n−Fks)p=49,5+(1510026(60)−7)5=49,5+(1515,6−7)5=49,5+(158,6)5=49,5+2,87=52,37
Jadi, nilai Persentil ke-26 (P26) usia di Desa Merdeka adalah 50,06 kg.
Mudah bukan?! 😄
 Kuartil 1 ()
Kuartil 1 ()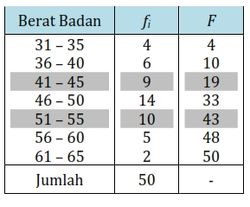


 Kuartil 1 (
Kuartil 1 (