Sudah pertengahan september nih, bagi kamu yang mau penilaian tengah semester atau PTS penulis bagikan beberapa soal ya untuk berlatih..
Sudah pertengahan september nih, bagi kamu yang mau penilaian tengah semester atau PTS penulis bagikan beberapa soal ya untuk berlatih..
Kali ini saya bagikan soal tentang dimensi tiga, ini materi kelas XII matematika umum. Sudah tau materinya belum?? kalau belum baca dulu materi tentang dimensi tiga. Di kelas XII materi dimensi tiga membahas tentang jarak titik, garis dan bidang. Silakan dicermati dulu materinya. Konsep jarak titik, garis dan bidang↝
1. Diketahui kubus ABCD.EFGH dengan panjang rusuk 24 cm. Titik P di tengah rusuk AF. Titik Q terletak di rusuk EF dengan perbandingan EQ:QF=1:3.
Diketahui kubus ABCD.EFGH dengan panjang rusuk 24 cm. Titik P di tengah rusuk AE. Titik Q terletak di rusuk EF dengan perbandingan EQ:QF=1:3. Hitunglah:
- Jarak titik Q ke titik C
- Jarak titik Q ke garis BG
- Jarak titik P ke bidang BDHF
- Jarak garis CG ke garis HB
- Jarak antara bidang ACH dan BEG
Alternatif Penyelesaian
Perhatikan gambar berikut
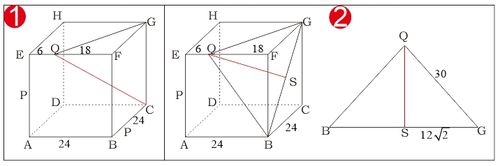 Diketahui panjang rusuk 24 cm, P ditengah AE dan
Diketahui panjang rusuk 24 cm, P ditengah AE dan
cm
cm
- Jarak titik Q ke titik C Jadi, Jarak titik Q ke titik C adalah cm.
- Jarak titik Q ke garis BG
Perhatikan sama kaki
cari panjang
Misal S proyeksi Q pada BG sehingga jarak titik Q ke garis BG adalah QS. BG merupakan diagonal bidang sehingga Panjang QS dapat dicari dengan menggunakan teorema pythagoras Jadi, Jarak titik Q ke garis BG adalah cm - Jarak titik P ke bidang BDHF
Perhatikan gambar berikut untuk nomor 3 dan 4 Jarak P ke bidang BDHF merupakan setengah dari diagonal bidang sehingga jaraknya cm
Jarak P ke bidang BDHF merupakan setengah dari diagonal bidang sehingga jaraknya cm - Jarak garis CG ke garis HB
Jarak CG ke garis HB merupakan setengah dari diagonal bidang sehingga jaraknya cm - Jarak antara bidang ACH dan BEG
Perhatikan gambar berikut untuk nomor 5 Jarak bidang ACH dan BEG adalah ruas garis SM, panjang ruas garis diagonal ruang. Sehingga
Jarak bidang ACH dan BEG adalah ruas garis SM, panjang ruas garis diagonal ruang. Sehingga
Jarak bidang ACH dan BEG = cm.
2. Diketahui balok ABCD.EFGH dengan panjang AB=28 cm, BC=18 cm, dan CG=24 cm. Titik P terletak pada HG dengan perbandingan HP:PG=3:5.
Diketahui balok ABCD.EFGH dengan panjang AB=32 cm, BC=18 cm, dan CG=24 cm. Titik P terletak pada HG dengan perbandingan HP:PG=3:5. Hitunglah
- Jarak titik A ke titik P
- Jarak titik C ke garis BD
- Jarak garis FG ke bidang BCHE
Alternatif Penyelesaian
Perhatikan gambar berikut untuk soal 1 dan 2
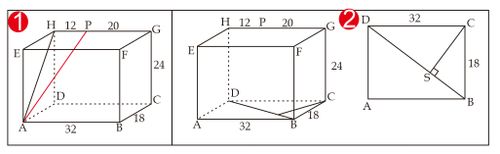 Diketahui balok ABCD.EFGH
Diketahui balok ABCD.EFGH
cm,
cm
cm
Titik pada dengan sehingga
cm
cm
- Jarak titik A ke titik P
Jarak titik A ke P merupakan panjang ruas garis AP sehingga Jadi, Jarak titik A ke P adalah cm - Jarak titik C ke garis BD
Perhatikan gambar 2 .
Misal S adalah proyeksi titik C pada garis BD sehingga jarak titik C ke garis BD adalah ruas garis CS. Cari panjang BD dengan pythagoras Pada berlaku kesamaan luas segitiga. Jadi, jarak titik C ke garis BD adalah cm. - Jarak garis FG ke bidang BCHE
Perhatikan gambar berikut. Misal Q adalah salah satu titik hasil proyeksi titik garis FG pada bidang BCHE, maka jarak garis FG ke bidang BCHE adalah panjang ruas garus FQ.
Misal Q adalah salah satu titik hasil proyeksi titik garis FG pada bidang BCHE, maka jarak garis FG ke bidang BCHE adalah panjang ruas garus FQ.
Cari panjang BE dengan pythagoras Pada berlaku kesamaan luas segitiga. Jadi, jarak garis FG ke bidang BCHE adalah cm.
3. Diketahui limas segiempat beraturan T.ABCD dengan panjang rusuk alas 24 cm dan rusuk tegak 20 cm.
Diketahui limas segiempat beraturan T.ABCD dengan panjang rusuk alas 24 cm dan rusuk tegak 20 cm. Hitunglah
- jarak titik C ke bidang alas.
- jarak titik B ke garis TD.
Alternatif Penyelesaian
Perhatikan gambar berikut untuk soal 1 dan 2
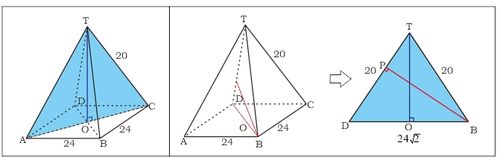
- jarak titik C ke bidang alas.
Misal O pada alas sehingga jarak titik C ke bidang alas adalah panjang ruas garis TO.
AC diagonal bidang alas sehingga cm. Jadi, jarak titik C ke bidang alas adalah - jarak titik B ke garis TD.
Misal P adalah proyeksi B pada TD maka jarak B ke TD adalah panjang ruas garis BP.
Perhatikan sama kaki. BP dapat diperolehdari kesamaan luas . jadi, jarak titik B ke garis TD adalah cm.
Demikian, beberapa soal tentang dimensi tiga. Semoga PTSnya berjalan lancar dan mendapat nilai yang maksimal ya..
Semua terasa mudah jika kita terbiasa dan banyak berlatih..
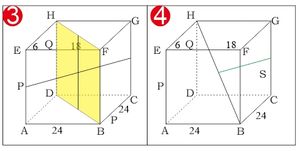 Jarak P ke bidang BDHF merupakan setengah dari diagonal bidang sehingga jaraknya
Jarak P ke bidang BDHF merupakan setengah dari diagonal bidang sehingga jaraknya 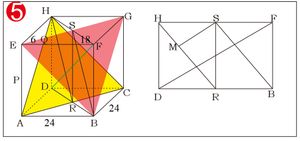 Jarak bidang ACH dan BEG adalah ruas garis SM, panjang ruas garis
Jarak bidang ACH dan BEG adalah ruas garis SM, panjang ruas garis 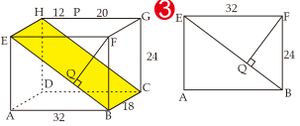 Misal Q adalah salah satu titik hasil proyeksi titik garis FG pada bidang BCHE, maka jarak garis FG ke bidang BCHE adalah panjang ruas garus FQ.
Misal Q adalah salah satu titik hasil proyeksi titik garis FG pada bidang BCHE, maka jarak garis FG ke bidang BCHE adalah panjang ruas garus FQ.