belajar bagaimana menentukan fungsi eksponen jika diketahui gambar grafiknya
Terkadang kita menemukan soal yang diminta untuk menentukan fungsi dari suatu grafik….
Nah, pada artikel kali ini kita akan belajar bagaimana menentukan fungsi eksponen jika diketahui gambar grafiknya. Sebelum lanjut silahkan teman-teman pelajari dulu tentang garfik fungsi eksponen ya Mengambar Grafik Fungsi Eksponen↝
Agar lebih mudah dalam memahami materi menentukan fungsi eksponen dari grafiknya, teman-tean perlu kuasai dulu sifat eksponen, bentuk fungsi eksponen, dan juga menyelesaikan sistem persamaan. Setelah dikuasai, yuk kita ikuti pembahasan berikut ini.
Menentukan Fungsi Eksponen dari Grafiknya
Secara umum bentuk dari fungsi eksponen yang kita bahas ini adalah
f(x)=k⋅ax+c akan tetapi kadang kita juga hanya sampai bentuk
f(x)=k⋅ax.
Catatan
- Jika grafik eksponen yang diketahui hanya terdiri dari dua titik maka kita gunakan fungsi f(x)=k⋅ax
- Jika grafik fungsi eksponen yang diketahui terdiri lebih dari dua titik maka kita gunakan fungsi f(x)=k⋅ax+c
Contoh Soal Menentukan Fungsi Eksponen dari Grafiknya 1
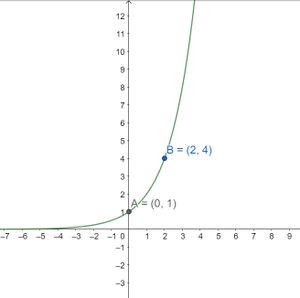
Tentukan fungsi eksponen dari grafik berikut ini.
 Alternatif Penyelesaian :
Alternatif Penyelesaian :
Grafik pada gambar contoh soal diatas melalui dua titik yaitu (0,1) dan (2,4), sehingga kita gunakan fungsi f(x)=k⋅ax.
Kita substitusikan kedua titik tersebut ke f(x)=y=k⋅ax.
(x,y)=(0,1)→y111=k⋅ax=k⋅a0=k⋅1=k
Sehingga fungsinya menjadi :
f(x)=k⋅ax→f(x)=1⋅ax→f(x)=ax.
Selanjutnya kita substitusi titik (2,4)
(x,y)=(2,4)→y4222=ax=a2=a2=a
Sehingga fungsinya :
f(x)=ax→f(x)=2x.
Jadi, fungsi eksponen dari grafik tersebut adalah f(x)=2x.
Tentukan fungsi eksponen dari grafik berikut ini.
 Alternatif Penyelesaian :
Alternatif Penyelesaian :
Grafik diatas melalui dua titik yaitu (2,1) dan (1,4), sehingga kita gunakan fungsi f(x)=k⋅ax.
Kita substitusikan kedua titik tersebut ke f(x)=y=k⋅ax.
(x,y)=(2,1)→y1a21k=k⋅ax=k⋅a2=k=a21 …pers(i)
Selanjutnya substitusi titik (1,4)
(x,y)=(1,4)→y4k⋅ak=k⋅ax=k⋅a1=4=a4 …pers(ii)
Selanjutnya substitusi pers (i) k=a21 ke pers (ii)
k=a21→ka21a4a2−aa(4a−1)a=0a=0=a4=a4=4a2=0=0 atau 4a−1=0 atau a=41
untuk nilai a=0 tidak mememnuhi karena basis a=0 tidak memenuhi syarat. sehingga a yang mungkin hanya a=41.
Selanjutnya substitusi a=41 ke pers(ii)
a=41→kk kk=a4=414=414=42
Sehingga fungsinya :
f(x)=k⋅ax→f(x)f(x)f(x)=42⋅(41)x=(41)−2⋅(41)x=(41)x−2
Jadi, fungsi eksponen dari grafik tersebut adalah f(x)=(41)x−2.
Tentukan fungsi eksponen dari grafik berikut ini.
 Alternatif Penyelesaian :
Alternatif Penyelesaian :
Grafik diatas melalui dua titik yaitu (1,2) dan (2,6), sehingga kita gunakan fungsi f(x)=k⋅ax.
Kita substitusikan kedua titik tersebut ke f(x)=y=k⋅ax.
(x,y)=(1,2)→y2a2k=k⋅ax=k⋅a1=k=a2 …pers(i)
Selanjutnya substitusi titik (2,6)
(x,y)=(2,6)→y6k⋅a2k=k⋅ax=k⋅a2=6=a26 …pers(ii)
Selanjutnya substitusi pers (ii) k=a26 ke pers (i)
k=a26→ka266a2a2−6a2a(a−3)a=0a=0=a2=a2=2a2=0=0 atau a−3=0 atau a=3
untuk nilai a=0 tidak mememnuhi karena basis a=0 tidak memenuhi syarat. sehingga a yang mungkin hanya a=3.
Selanjutnya substitusi a=3 ke pers(i)
a=3→kk kk=a2=32=312=2⋅3−1
Sehingga fungsinya :
f(x)=k⋅ax→f(x)f(x)=2⋅3−1⋅3x=2⋅3x−1
Jadi, fungsi eksponen dari grafik tersebut adalah f(x)=2⋅3x−1.
Contoh Soal Menentukan Fungsi Eksponen dari Grafiknya 2
- Tentukan fungsi eksponen dari grafik berikut ini.
 Alternatif Penyelesaian :
Alternatif Penyelesaian :
Grafik diatas melalui tiga titik yaitu (0,4), (1,7) dan (2,13), sehingga kita gunakan fungsi f(x)=k⋅ax+c.
Kita substitusikan ketiga titik tersebut ke f(x)=y=k⋅ax+c.
Substitusi titik (0,4)
(x,y)=(0,4)→y44k+c=k⋅ax+c=k⋅a0+c=k+c=4 …pers(i)
Substitusi titik (1,7)
(x,y)=(1,7)→y77k⋅a+c=k⋅ax+c=k⋅a1+c=k⋅a+c=7 …pers(ii)
Substitusi titik (2,13)
(x,y)=(2,13)→y13k⋅a2+c=k⋅ax+c=k⋅a2+c=7 …pers(iii)
Selanjutnya Eliminasi pers(i) dan pers(ii) :
k⋅a+ck+ck⋅a−k=7=4=3
Kita peroleh : k⋅a−k=3 ….pers(iv).
Eliminasi pers(ii) dan pers(iii) :
k⋅a2+ck⋅a+ck⋅a2−k⋅aa(k⋅a−k)=13=7=6=6
Kita peroleh : a(k⋅a−k)=6 ….pers(v).
Dari pers(iv) dan (v),
⇔⇔a(k⋅a−k)=6a×3=6a=2
Pers(iv) : k⋅a−k=3⇔2k−k=3⇔k=3.
Pers(i) : k+c=4⇔3+c=4⇔c=1.
Sehingga fungsinya : f(x)=k⋅ax+c=3⋅2x+1.
Jadi, fungsi eksponen dari grafik tersebut adalah f(x)=3⋅2x+1.
Demikian artikel mengenai menentukan fungsi eksponen jika diketahui grafiknya, selanjutnya yuk pelajari hubungan antara dua grafik fungsi eksponen↝
 Alternatif Penyelesaian :
Alternatif Penyelesaian : Alternatif Penyelesaian :
Alternatif Penyelesaian : Alternatif Penyelesaian :
Alternatif Penyelesaian : Alternatif Penyelesaian :
Alternatif Penyelesaian :
 Alternatif Penyelesaian :
Alternatif Penyelesaian : Alternatif Penyelesaian :
Alternatif Penyelesaian :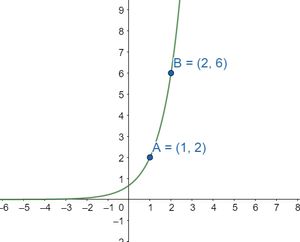 Alternatif Penyelesaian :
Alternatif Penyelesaian :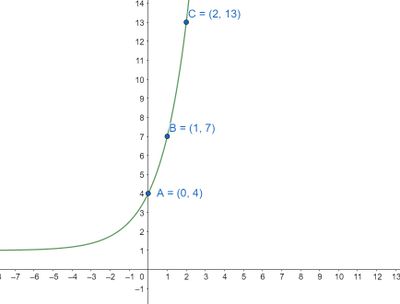 Alternatif Penyelesaian :
Alternatif Penyelesaian :