Trigonometri dasar adalah materi prasyarat untuk belajar persamaan trigonometri. perbedaan aplikasi perbandingan trigonometri dan persamaan trigonometri? Dalam aplikasi perbandingan trigonometri biasanya yang ditentukan adalah jarak atau tinggi dengan besar sudut yang sudah diketahui, misalnya nilai dari sin x, cos x, dan tan x dan seterusnya yang sudah diketahui.

Daftar Isi

Apakah kalian tahu perbedaan aplikasi perbandingan trigonometri dan persamaan trigonometri? Dalam aplikasi perbandingan trigonometri biasanya yang ditentukan adalah jarak atau tinggi dengan besar sudut yang sudah diketahui, misalnya nilai dari sin x, cos x, dan tan x dan seterusnya yang sudah diketahui. Contohnya adalah penentuan jarak antara dua benda, tinggi tiang bendera, tinggi pohon atau tinggi menara. Sebaliknya, pada aplikasi persamaan trigonometri kalian justru diminta menentukan besar sudut x yang terdapat dalam perbandingan trigonometri. Seringkali besar sudut yang memenuhi tidaklah tunggal.

Persamaan trigonometri banyak diterapkan dalam kehidupan sehari-hari. Dalam bidang fisika contohnya adalah fungsi periodik gelombang cahaya, gelombang bunyi, dan menentukan kecepatan sudut suatu partikel. Untuk menentukan kecepatan sudutnya, kamu harus melihat persamaan gerak partikel tersebut. Kata kunci yang harus kamu perhatikan adalah kecepatan sudut. Partikel yang memiliki kecepatan sudut, pasti persamaan geraknya adalah persamaan trigonometri.

Penerapan persamaan trigonometri dalam bidang pembangunan contohnya adalah melakukan survei pembuatan jalan, pembuatan jembatan dan mendirikan bangunan, semua itu menggunakan trigonometri dalam pekerjaannya sehari-hari. Pembangunan jalan pasti juga akan mempertimbangan kemiringan suatu sudut pada permukaan tanah. Dalam pembangunan jalan, permukaan lapis pondasi harus rata sehingga air tidak dapat menggenang akibat permukaan yang tidak rata. Deviasi maksimum untuk kerataan permukaan adalah 1 cm.

Maka dari itu, ilmu trigonometri sangat berperan dalam proyek pembangunan suatu jalan, tidak perlu susah-susah harus mengukur luasnya lahan yang akan kita bangun dengan terjun ke medan tersebut. Tapi, hanya dengan kita mengambil data dan diinput dalam suatu system informasi serta dengan ilmu trigonometri kita dapat mengukur kemiringan suatu permukaan tanah. Sebelum belajar persamaan trigonometri ada materi prasyarat yang harus kamu pahami dengan benar, yaitu terkait materi trigonometri dasar. Mari kita mulai dengan mengingat kembali dasar-dasar trigonometri.

Konsep dasar Trigonometri

Perbandingan trigonometri dalam segitiga siku-siku

Perhatikan segitiga siku-siku berikut

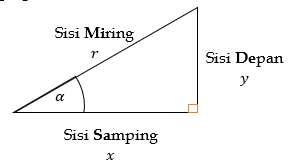
segitiga siku-siku

Gambar 1. Segitiga Siku-siku

Berdasarkan segitiga siku-siku di atas didefinisikan perbandingan trigonometri sebagai berikut :

$$\sin \alpha =\frac{y}{r}=\frac{\text{sisi depan}}{\text{sisi miring}}=\frac{de}{mi}$$

$$\cos \alpha =\frac{x}{r}=\frac{\text{sisi samping}}{\text{sisi miring}}=\frac{sa}{mi}$$

$$\tan \alpha =\frac{y}{x}=\frac{\text{sisi depan}}{\text{sisi samping}}=\frac{de}{sa}$$

Contoh:

Diketahui $\alpha $ sudut lancip dan $\sin \alpha =\frac{3}{5}$ . Tentukan besar sudutnya dan nilai dari $\cos \alpha $ dan $\tan \alpha $!

Alternatif Penyelesaian

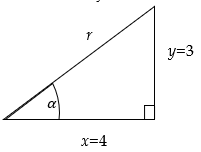
contoh soal trigonometri dasar

Nilai r dicari dengan menggunakan teorema pythagoras $$r=\sqrt{{{x}^{2}}+{{y}^{2}}} $$ $$ r=\sqrt{{{4}^{2}}+{{3}^{2}}} $$ $$ r=\sqrt{25}=5 $$ nilai $\cos \alpha =\frac{x}{r}=\frac{4}{5}$ dan nilai $\tan \alpha =\frac{y}{x}=\frac{3}{4}$

Untuk mencari besar sudut digunakan $\alpha ={{\sin }^{-1}}(\frac{3}{5})$
(dibaca: antisin dari $\frac{3}{5}$).
Dengan menggunakan tabel trigonometri diperoleh $\alpha =36,87{}^\circ =36{}^\circ 52'\approx 37{}^\circ $.

Identitas Trigonometri

Identitas trigonometri adalah bentuk persamaan trigonometri yang menghubungkan suatu perbandingan trigonometri dengan perbandingan trigonometri yang lainnya.

Ada tiga jenis identitas trigonometri, yaitu :

  1. Hubungan kebalikan $$\secā” x=\frac{1}{\cosā” x}$$ $$\cscā” x=\frac{1}{\sinā” x} $$ $$\cotā” x=\frac{1}{\tan x} $$
  2. Hubungan perbandingan $$\tan ā”A=\frac{\sin ā”A}{\cos ā”A }$$
  3. Hubungan pythagoras $${{\sin }^{2}}x+{{\cos }^{2}}x=1 $$ $${{\tan }^{2}}x+1\text{ }={{\sec }^{2}}x $$ $$ 1+{{\cot }^{2}}x={{\csc }^{2}}x$$

Selain identitas dasar di atas, identitas-identitas yang lain dapat dikembangkan dengan memanfaatkan rumus identitas dasar tersebut. Untuk menunjukkan kebenaran suatu identitas trigonometri dapat dilakukan dengan mengubah salah satu atau kedua ruas persamaan menjadi bentuk yang sama. Atau ruas kiri dirubah sehingga sama dengan ruas kanan atau ruas kanan dirubah sehingga sama dengan ruas kiri. Perhatikan contoh soal berikut ini

Contoh

Buktikan bahwa $\frac{1-\sin \alpha }{\cos \alpha }=\frac{\cos \alpha }{1+\sin \alpha }$!

Bukti

Ruas kiri $=\frac{1-\sin \alpha }{\cos \alpha }$
Ruas kiri $ =\left( \frac{1-\sin \alpha }{\cos \alpha } \right)\left( \frac{1+\sin \alpha }{1+\sin \alpha } \right) $
Ruas kiri $=\frac{1-{{\sin }^{2}}\alpha }{\cos \alpha \left( 1+\sin \alpha \right)} $
Ruas kiri $ =\frac{{{\cos }^{2}}\alpha }{\cos \alpha \left( 1+\sin \alpha \right)} $
Ruas kiri $ =\frac{\cos \alpha }{1+\sin \alpha } $
Ruas kiri = Ruas kanan

Perbandingan trigonometri sudut istimewa di kuadran I

Untuk memahami berapa nilai perbandingan trigonometri untuk sudut istimewa, kalian hanya perlu memahami perbandingan sudut pada segitiga berikut ini.

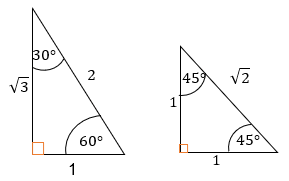
perbandingan segitiga sudut istimewa

Gambar 2. Perbandingan segitiga sudut istimewa

Dari gambar diatas dapat dibuat tabel untuk nilai perbandingan trigonometri sudut istimewa.

Īøsinā”Īøcosā”Īøtanā”Īø
$0{}^\circ $010
$30{}^\circ $$\frac{1}{2}$$\frac{1}{2}\sqrt{3}$$\frac{1}{3}\sqrt{3}$
$45{}^\circ $$\frac{1}{2}\sqrt{2}$$\frac{1}{2}\sqrt{2}$1
$60{}^\circ $$\frac{1}{2}\sqrt{3}$$\frac{1}{2}$$\sqrt{3}$
$90{}^\circ $10Tidak terdefinisi

Tabel 1. Nilai perbandingan trigonometri sudut istimewa

Perbandingan trigonometri sudut berelasi

Sudut satu lingkaran terbagi menjadi 4 wilayah ( kuadran), yaitu :

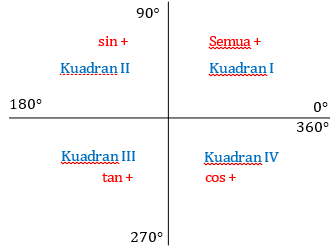
perbandingan sudut trigonometri diberbagai kuadran

Gambar 3. Sudut diberbagai kuadran

  1. Sudut-sudut yang terletak di kuadran I, yaitu sudut-sudut yang besarnya antara $0^\circ $ sampai $90{}^\circ $ atau $0{}^\circ <\alpha {}^\circ <90{}^\circ $ atau sudut lancip.
  2. Sudut-sudut yang terletak di kuadran II, yaitu sudut-sudut yang besarnya antara $90{}^\circ $ sampai $180{}^\circ $ atau $90{}^\circ <\alpha {}^\circ <180{}^\circ $ atau sudut tumpul.
  3. Sudut-sudut yang terletak di kuadran III, yaitu sudut-sudut yang besarnya antara $180{}^\circ $ sampai $270{}^\circ $ atau $180{}^\circ <\alpha {}^\circ <270{}^\circ $.
  4. Sudut-sudut yang terletak di kuadran IV, yaitu sudut-sudut yang besarnya antara $270{}^\circ $ sampai 360o atau $270{}^\circ <\alpha {}^\circ <360{}^\circ $.

Perhatikan tanda (+) pada masing-masing kuadran di atas, dapat diperoleh tabel tanda nilai perbandingan trigonometri sebagai berikut : Fungsi Trigonometri Kuadran

IIIIIIIV
$\sin \alpha $++--
$\cos \alpha $+--+
$\tan \alpha $+-+-

Tabel 2. Tabel Tanda Nilai Perbandingan Trigonometri

Nilai perbandingan trigonometri untuk sudut-sudut istimewa dapat dikelompokkan menjadi dua bagian, yakni :

  1. Dengan menggunakan aturan pelurus $(180{}^\circ -\alpha {}^\circ )$, $(180{}^\circ +\alpha {}^\circ )$ dan $(360{}^\circ -\alpha )$. Dalam aturan ini bentuk perbandingan trigonometri tidak mengalami perubahan.
  2. Dengan menggunakan aturan penyiku $(90{}^\circ +\alpha {}^\circ )$, $(270{}^\circ -\alpha )$ dan $(270{}^\circ +\alpha )$. Dalam aturan ini bentuk perbandingan trigonometri mengalami perubahan yaitu bentuk sin menjadi cos, bentuk cos menjadi sin, bentuk tan menjadi cot.

Contoh:

Tentukanlah nilai dari :

  1. $\cos 150{}^\circ $
  2. $\sin 225{}^\circ $

Alternatif Penyelesaian:

  1. $\cos 150{}^\circ =\cos (180{}^\circ -30{}^\circ )$
    $=-\cos 30{}^\circ $
    $ =-\frac{1}{2}\sqrt{3} $
  2. $\sin 225{}^\circ =\sin (270{}^\circ -45{}^\circ )$
    $ =-\cos 45{}^\circ $
    $ =-\frac{1}{2}\sqrt{2} $

Aturan Periodisitas Trigonometri

Untuk menentukan nilai perbandingan trigonometri terhadap sudut-sudut yang besarnya lebih dari $360{}^\circ $ maka digunakanlah aturan periodisitas trigonometri. Nilai sinus dan cosinus akan berulang setiap kelipatan $360{}^\circ $ sedangkan nilai tangens akan berulang setiap $180{}^\circ $ . ini berati $\sin 30{}^\circ =\sin 390{}^\circ =\sin 750{}^\circ $ dan seterusnya. Sehingga dapat dirumuskan : $$\sin (k.360{}^\circ +\alpha )=\sin \alpha $$ $$\cos (k.360{}^\circ +\alpha )=\cos \alpha $$ $$\tan (k.180{}^\circ +\alpha )=\tan \alpha $$ dimana $k$ adalah bilangan bulat

Namun dalam praktiknya aturan periodisitas di atas dapat disederhanakan dengan rumusan :

$$\sin (\alpha -k.360{}^\circ )=\sin \alpha $$ $$\cos (\alpha -k.360{}^\circ )=\cos \alpha $$ $$\tan (\alpha -k.360{}^\circ )=\tan \alpha $$ dimana $k$ adalah bilangan bulat dan $k.360{}^\circ \ge 360{}^\circ $.

Contoh

Tentukanlah nilai dari

  1. $\sin (-315){}^\circ $
  2. $\cos (-\frac{4}{3}\pi )$
  3. $\tan 600{}^\circ $

Jawab

  1. $\sin (-315){}^\circ =\sin (-315{}^\circ +360{}^\circ )$
    $=\sin 45{}^\circ $
    $=\frac{1}{2}\sqrt{2} $

  2. $\cos (-\frac{4}{3}\pi )=\cos (-\frac{4}{3}\times 180{}^\circ )$
    $=\cos (-240{}^\circ ) $
    $=\cos (-240{}^\circ +360{}^\circ ) $
    $=\cos (120{}^\circ ) $
    $=\cos (180{}^\circ -60{}^\circ ) $
    $=-\cos 60{}^\circ $
    $=-\frac{1}{2} $

  3. $\tan 600{}^\circ =\tan (600{}^\circ -360{}^\circ )$
    $=\tan 240{}^\circ $
    $=\tan (180{}^\circ +60{}^\circ ) $
    $=\tan 60{}^\circ $
    $=\sqrt{3} $